-
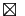 Si
Si  admet une limite finie en
admet une limite finie en  alors
alors  est bornée au voisinage de
est bornée au voisinage de
 .
.
 Si
Si  admet une limite finie en
admet une limite finie en  alors
alors  est monotone au voisinage de
est monotone au voisinage de
 .
.
-
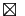 Si
Si  admet une limite en
admet une limite en  , alors
, alors  admet une limite à droite
en
admet une limite à droite
en  .
.
 Si
Si  admet une limite à gauche et une limite à droite en
admet une limite à gauche et une limite à droite en  alors
alors  admet une limite en
admet une limite en  .
.
-
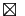
 admet
admet 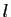 pour limite à gauche et pour limite à droite en
pour limite à gauche et pour limite à droite en
 si et seulement si
si et seulement si 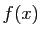 tend vers
tend vers 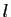 quand
quand 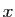 tend vers
tend vers  .
.
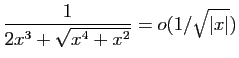
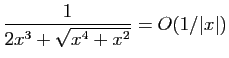
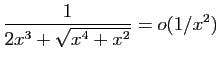
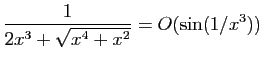
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales