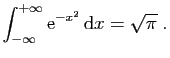
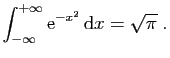
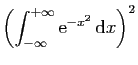 |
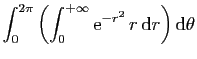 |
||
![$\displaystyle \displaystyle{
\int_0^{2\pi} \left[-\frac{\mathrm{e}^{-r^2}}{2}\right]_0^{+\infty} \mathrm{d}\theta }$](img601.gif) |
|||
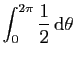 |
|||
Auparavant, P.S. Laplace (1749-1827) avait été le premier en 1774 à fournir un calcul rigoureux. La fonction à intégrer étant paire,
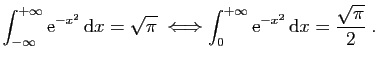
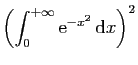 |
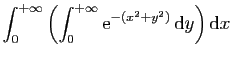 |
||
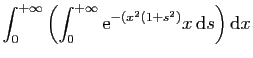 |
|||
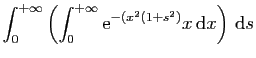 |
|||
![$\displaystyle \displaystyle{
\int_0^{+\infty}\left[-\frac{1}{2(1+s^2)}\mathrm{e}^{-x^2(1+s^2)}\right]_0^{+\infty} \mathrm{d}s }$](img610.gif) |
|||
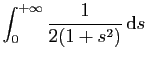 |
|||
![$\displaystyle \displaystyle{
\left[\frac{1}{2}\arctan(s)\right]_0^{+\infty} =\frac{\pi}{4}}$](img612.gif) |
Au reste, ce principe, dont nous avons fait usage depuis 1795, a été donné dernièrement par Legendre dans ses Nouvelles méthodes pour la détermination des orbites des comètes, Paris 1805 ; on trouvera dans cet ouvrage plusieurs conséquences que le désir d'abréger nous a fait omettre.Cette citation négligente eut le don d'agacer sérieusement Legendre, qui répliqua.
Je ne vous dissimulerai donc pas, Monsieur, que j'ai éprouvé quelque regret de voir qu'en citant mon mémoire..., vous dites principum nostrum... Il n'est aucune découverte qu'on ne puisse s'attribuer en disant qu'on avait trouvé la même chose quelques années auparavant ; mais si on n'en fournit pas la preuve en citant le lieu où on l'a publiée, cette assertion devient sans objet et n'est plus qu'une chose désobligeante pour le véritable auteur de la découverte. En Mathématiques il arrive très souvent qu'on trouve les mêmes choses qui ont été trouvées par d'autres et qui sont bien connues ; c'est ce qui m'est arrivé nombre de fois, mais je n'en ai point fait mention et je n'ai jamais appelé principum nostrum un principe qu'un autre avait publié avant moi. Vous êtes assez riche de [votre] fond, Monsieur, pour n'avoir rien à envier à personne ; et [je suis] bien persuadé au reste que j'ai à me plaindre de l'expression seulement et nullement de l'intention...Mais Gauss persiste et signe.
Je n'avais pas l'idée, que M. Legendre pouvait attacher tant de prix à une idée aussi simple, qu'on doit plutôt s'étonner qu'on ne l'a pas eue depuis 100 ans, pour se fâcher que je raconte, que je m'en suis servi avant lui ?Le différent n'est toujours pas réglé. Sans vouloir jeter de l'huile sur le feu, un troisième larron, beaucoup moins connu que les deux précédents, a lui aussi publié la méthode des moindres carrés, en 1808 sans connaître les travaux des deux autres. Il s'agit de Robert Adrain (1775-1863), mathématicien américain d'origine irlandaise. Comme le dit B. Hayes 1,
One obvious fact is that it can be very hard to get noticed when you are standing on the farther shore of the ocean, no matter how vigorously you wave your arms. Another truth, even more bitter, is that it's also very hard in those circumstances to do anything worth noticing. And yet there is a more cheerful outlook, at least for those who can afford to be patient: The world turns, and eventually the farther shore may become the center.Sachez aussi que Adrain s'est fait licencier (à 59 ans) de son poste à l'université, car il ne parvenait pas à maintenir la discipline dans ses cours.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales