Projection stéréographique et homographies

Une projection qui est moins utilisée par les géographes, mais qui présente de remarquables propriétés mathématiques, est la projection stéréographique.

On projette la surface de la terre, assimilée à la sphère unité, sur le plan de l'équateur par une projection centrale de centre le pôle Nord. Par tout point de la terre distinct du pôle Nord , on trace donc la droite , qui coupe le plan de l'équateur en un unique point .

$\includegraphics[width=0.7\textwidth]{stereo}$

Si on rapporte l'espace à un repère orthonormé d'origine le centre de la sphère et tel que ait pour coordonnées , cette transformation est donnée en formules par

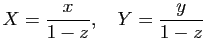
$\displaystyle X=\dfrac{x}{1-z}, \quad Y=\dfrac{y}{1-z}$

où

sont les coordonnées du point

celles du point

dans le plan

. L'application

est une bijection de la sphère privée du point

sur le plan

et la bijection réciproque est donnée par

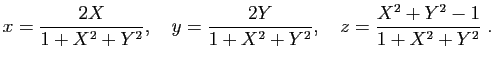
$\displaystyle x=\dfrac{2X}{1+X^2+Y^2}, \quad y=\dfrac{2Y}{1+X^2+Y^2}, \quad z=\dfrac{X^2+Y^2-1}{1+X^2+Y^2} \; .$

Ces formules permettent de montrer que l'image par de tout cercle tracé sur la sphère est une droite ou un cercle : plus précisément, c'est une droite si le cercle passe par et un cercle sinon.

Si on identifie le plan au corps des nombres complexes en associant à chaque point son affixe, on obtient ainsi une bijection de la sphère privée du point sur $\mathbb{C}$ . Pour obtenir une bijection définie sur la sphère tout entière, on complète $\mathbb{C}$ par un point à l'infini : en effet, quand un point de la sphère s'approche de , son image s'éloigne à l'infini.

Le plan complexe ainsi complété, noté $\mathbb{\hat C}$ , est appelé sphère de Riemann et constitue le cadre naturel pour étudier les homographies.

Une homographie est une application 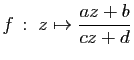$f\, :\; z\mapsto \dfrac{az+b}{cz+d}$ où sont des nombres complexes vérifiant $ad-bc \not = 0$ (sinon l'application serait constante). Cette application définit, si $c\not =0$ , une bijection de $\mathbb{C}$ privé du point sur $\mathbb{C}$ privé du point (si , c'est une similitude directe). On la complète en une bijection de $\mathbb{\hat C}$ sur $\mathbb{\hat C}$ en posant $f(-d/c)=\infty$ et $f(\infty)=a/c$ . Elle a la propriété de transformer une droite ou un cercle en une droite ou un cercle.

Projection stéréographique et projection de Mercator

Si on repère le point de la sphère par sa latitude $\theta$ et sa longitude $\varphi$ et son projeté sur le plan par ses coordonnées polaires et $\varphi$ , on voit sur la figure dans le plan que

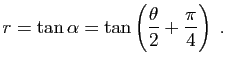
$\displaystyle r= \tan \alpha=\tan\left( \dfrac{\theta}{2}+\dfrac{\pi}{4} \right)\; .$

$\includegraphics[width=8cm]{stereoggb}$

L'affixe du point est donc

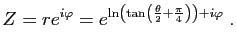
$\displaystyle Z=r e^{i\varphi}=e^{\ln \left( \tan \left( \frac{\theta}{2}+\frac{\pi}{4} \right) \right)+i\varphi} \; .$

Cette formule rappelle celle donnant les coordonnées de l'image de

par la projection de Mercator et ce n'est pas un hasard : en effet, si on échange les rôles de

dans les formules donnant la projection de Mercator (ce qui revient à noter

l'axe vertical et

l'axe horizontal) et si on note

l'affixe du point

, on obtient

. La projection stéréographique comme la projection de Mercator sont en effet des projections conformes (elles conservent les angles). Si on les restreint à la sphère privée de ses deux pôles, elles définissent des bijections respectivement sur $\mathbb{C}^*=\mathbb{C}\setminus\{0\}$ et sur la bande $\{z \mid -\pi < \mathrm{Im}(z) \leq \pi\}$ et la fonction exponentielle réalise précisément une bijection conforme entre ces deux domaines de $\mathbb{C}$ .

Pour en savoir plus sur la projection stéréographique et sur d'autres sujets abordés dans ces compléments (et sur bien d'autres choses encore), vous pouvez consulter le site : http://www.dimensions-math.org/Dim_fr.htm qui vous fera voyager jusque dans la quatrième dimension.