Courbes de Bézier

Une application très concrète, en dehors de la mécanique d'où elle est issue, de la notion de barycentre est fournie par l'étude des courbes de Bézier.

Pierre Bézier (1910-1999) était ingénieur chez Renault quand il introduisit en 1962 ces courbes et les surfaces qui portent également son nom pour modéliser des pièces d'automobile. À peu près à la même époque, Paul de Casteljau menait des études analogues chez Citroën, principal concurrent en France de Renault, et découvrait un algorithme récursif pour construire ces courbes, algorithme qui porte aujourd'hui son nom. Ces travaux, couverts par le secret industriel, ne furent publiés qu'une dizaine d'années plus tard.

Figure 6: Courbes de Bézier avec 3 et 4 points de contrôle

Pour simplifier, nous ne considérerons ici que le cas des courbes. Le problème d'interpolation le plus simple consiste à déterminer une courbe lisse passant par des points donnés et ayant une équation la plus simple possible. Bien sûr, s'il ne s'agit que de relier deux points donnés, la courbe la plus simple est le segment $[AB]$. Ce segment est l'ensemble des barycentres $(1-t)A+tB$ quand $t$ parcourt l'intervalle $[0,1]$. Quand on veut raccorder une suite de points, il faut pouvoir contrôler les tangentes aux points de raccordement. On ajoute pour cela un point de contrôle supplémentaire $C$, on note pour tout $t\in[0,1]$, $M=(1-t)A+tC$, $N=(1-t)C+tB$, $P=(1-t)M+tN$, de sorte que $P=(1-t)^2A+2t(1-t)C+t^2 B$. On vérifie alors facilement que la courbe décrite par le point $P$ quand $t$ parcourt $[0,1]$ est un arc de parabole joignant $A$ à $B$, admettant comme tangente en $A$ la droite $(AC)$ et comme tangente en $B$ la droite $(BC)$. Le point de contrôle supplémentaire $C$ permet donc de contrôler les tangentes aux deux extrémités de l'arc $AB$. Si on veut davantage de contrôle sur la forme de la courbe, on peut rajouter d'autres points de contrôle et itérer la construction précédente. 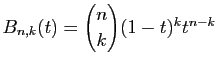La représentation paramétrique de la courbe obtenue fait alors intervenir les polynômes de Bernstein $B_{n,k}(t)=\dbinom{n}{k} (1-t)^kt^{n-k}$, qui apparaissent dans le développement de $[(1-t)+t]^n$ par la formule du binôme.

Comme toute application affine conserve les barycentres, pour construire l'image d'une courbe de Bézier par une application affine il suffit de prendre l'image des points de contrôle de la courbe initiale par l'application affine, l'image de la courbe de Bézier est alors la courbe de Bézier correspondant à ces points de contrôle, ce qui simplifie beaucoup la construction de cette image.

Les courbes de Bézier sont beaucoup utilisées dans les logiciels de dessin vectoriel et de création de polices de caractères. En particulier, le langage PostScript, dont la format pdf est largement issu, leur a accordé une grande place.