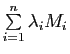 (pour
(pour
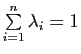 ) sont parfois appelées notations de Grassmann.
) sont parfois appelées notations de Grassmann.
Les notations ![]() et
et
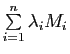 (pour
(pour
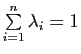 ) sont parfois appelées notations de Grassmann.
) sont parfois appelées notations de Grassmann.
Hermann Günther Grassmann (1809-1877) était un mathématicien et linguiste allemand. Enseignant de lycée pendant la majeure partie de sa vie professionnelle, l'importance de ses travaux mathématiques n'a été reconnue que tardivement et c'est pour ses études de sanskrit et notamment sa traduction en allemand du Rig-Véda qu'il devint célèbre à la fin de sa vie.
On le considère aujourd'hui comme un des inventeurs du calcul vectoriel et de l'algèbre linéaire (bien que des notions analogues à celle de vecteur soient apparues de manière récurrente, à l'état d'ébauche dès le XVIième siècle, puis de manière plus formelle au début du XIXième siècle, chez d'autres auteurs, l'idée étant à chaque fois de définir des grandeurs qui aient, outre une mesure, une direction et un sens).

Le calcul barycentrique lui-même avait en fait été introduit, à peu près à la même époque, par August Ferdinand Möbius (1790-1868) dans son livre Der barycentrische Calcül (1827). Dans cet ouvrage, Möbius (sans doute plus connu aujourd'hui pour sa découverte de la bande qui porte son nom, un exemple de surface non orientable plongée dans l'espace euclidien de dimension 3), introduisait non seulement les coordonnées barycentriques, mais aussi, en considérant le cas d'un système pondéré où la somme des poids est nulle, la notion de point à l'infini et les coordonnées projectives, ouvrant ainsi la voie à l'étude des relations entre espace affine et espace projectif.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales