Claude Ptolémée (90-168) était né à Ptolémaïs, en
Haute-Egypte, d'où son nom. Vers 150, il compila l'ensemble des
connaissances astronomiques de son temps dans une 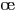 uvre magistrale,
la Composition Mathématique, rebaptisée plus tard
Almageste («le très grand») par
les savants arabes. Ce traité reprend et amplifie les connaissances
d'Hipparque de Nicée (180-125 av. JC).
Le système astronomique géocentrique de l'Almageste,
restera en vigueur jusqu'à la révolution copernicienne,
à la Renaissance.
uvre magistrale,
la Composition Mathématique, rebaptisée plus tard
Almageste («le très grand») par
les savants arabes. Ce traité reprend et amplifie les connaissances
d'Hipparque de Nicée (180-125 av. JC).
Le système astronomique géocentrique de l'Almageste,
restera en vigueur jusqu'à la révolution copernicienne,
à la Renaissance.
Calculer des distances en fonction d'angles observés est
l'activité de base de l'astronomie. Mais pour cela, les astronomes de
l'antiquité préféraient les cordes à nos sinus et cosinus
actuels. La notion de corde qui (sous-)tend un arc de
cercle est sans doute plus naturelle. Dans un cercle de rayon 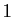 ,
notons
,
notons
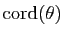 la longueur de la corde qui sous-tend
un arc de cercle d'angle
la longueur de la corde qui sous-tend
un arc de cercle d'angle 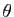 .
La figure 11 devrait
vous convaincre que :
.
La figure 11 devrait
vous convaincre que :
Figure:
La corde d'un angle 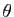 est le double du sinus de
l'angle moitié.
est le double du sinus de
l'angle moitié.
|
|
Dans le livre I, chapitre 9 de l'Almageste, on trouve le théorème
suivant.
Théorème 5 (de Ptolémée)
Dans un quadrilatère convexe inscrit dans un cercle, le produit des
diagonales est égal à la somme des produits des côtés opposés.
Nous vous laissons le plaisir de démontrer que ce théorème est
équivalent à la formule de sommation des sinus :
Il permit à Ptolémée de construire une table de cordes,
précise au demi-degré.
Les mathématiciens et astronomes arabes ne se contentèrent pas de
recopier, traduire et transmettre l' uvre de Ptolémée. Ils la
prolongèrent sur bien des points. Citons en particulier Abu al Wafa
et Al Biruni, qui systématisèrent l'usage du cercle
trigonométrique (de rayon
uvre de Ptolémée. Ils la
prolongèrent sur bien des points. Citons en particulier Abu al Wafa
et Al Biruni, qui systématisèrent l'usage du cercle
trigonométrique (de rayon 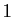 ), ainsi que Al Khwarizmi et Al
Battani, qui imposèrent l'usage des demi-cordes (notre sinus de
l'angle moitié), emprunté aux astronomes indiens (notamment
Aryabhata (476-550)).
), ainsi que Al Khwarizmi et Al
Battani, qui imposèrent l'usage des demi-cordes (notre sinus de
l'angle moitié), emprunté aux astronomes indiens (notamment
Aryabhata (476-550)).
L' uvre d'Al Battani (858-929) «le Ptolémée arabe», fut
traduite en latin, et rééditée au XVe siècle par Johann
Müller (1436-1476), qui étant natif de Königsberg, prit le nom
de Regiomontanus. Léonard de Pise (Fibonacci 1175-1250) semble
être le premier à avoir utilisé le mot latin
sinus qui semble venir du latin signifiant «repli».
En réalité, «corde » en sanscrit se dit «jiva», et «
jiba» en arabe signifie aussi «poche, repli de vêtement».
Un mauvaise traduction semble être l'origine de
ce glissement sémantique plutôt heureux, eût égard à
la forme sinueuse de la sinusoïde...
qui ne fut tracée et étudiée
en tant que telle que plusieurs siècles plus tard !
uvre d'Al Battani (858-929) «le Ptolémée arabe», fut
traduite en latin, et rééditée au XVe siècle par Johann
Müller (1436-1476), qui étant natif de Königsberg, prit le nom
de Regiomontanus. Léonard de Pise (Fibonacci 1175-1250) semble
être le premier à avoir utilisé le mot latin
sinus qui semble venir du latin signifiant «repli».
En réalité, «corde » en sanscrit se dit «jiva», et «
jiba» en arabe signifie aussi «poche, repli de vêtement».
Un mauvaise traduction semble être l'origine de
ce glissement sémantique plutôt heureux, eût égard à
la forme sinueuse de la sinusoïde...
qui ne fut tracée et étudiée
en tant que telle que plusieurs siècles plus tard !
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() ,
notons
,
notons
![]() la longueur de la corde qui sous-tend
un arc de cercle d'angle
la longueur de la corde qui sous-tend
un arc de cercle d'angle ![]() .
La figure 11 devrait
vous convaincre que :
.
La figure 11 devrait
vous convaincre que :
![]() uvre d'Al Battani (858-929) «le Ptolémée arabe», fut
traduite en latin, et rééditée au XVe siècle par Johann
Müller (1436-1476), qui étant natif de Königsberg, prit le nom
de Regiomontanus. Léonard de Pise (Fibonacci 1175-1250) semble
être le premier à avoir utilisé le mot latin
sinus qui semble venir du latin signifiant «repli».
En réalité, «corde » en sanscrit se dit «jiva», et «
jiba» en arabe signifie aussi «poche, repli de vêtement».
Un mauvaise traduction semble être l'origine de
ce glissement sémantique plutôt heureux, eût égard à
la forme sinueuse de la sinusoïde...
qui ne fut tracée et étudiée
en tant que telle que plusieurs siècles plus tard !
uvre d'Al Battani (858-929) «le Ptolémée arabe», fut
traduite en latin, et rééditée au XVe siècle par Johann
Müller (1436-1476), qui étant natif de Königsberg, prit le nom
de Regiomontanus. Léonard de Pise (Fibonacci 1175-1250) semble
être le premier à avoir utilisé le mot latin
sinus qui semble venir du latin signifiant «repli».
En réalité, «corde » en sanscrit se dit «jiva», et «
jiba» en arabe signifie aussi «poche, repli de vêtement».
Un mauvaise traduction semble être l'origine de
ce glissement sémantique plutôt heureux, eût égard à
la forme sinueuse de la sinusoïde...
qui ne fut tracée et étudiée
en tant que telle que plusieurs siècles plus tard !
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales