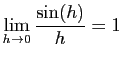 et
et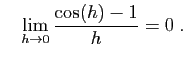
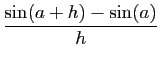 |
|||
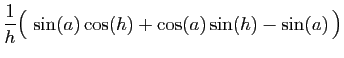 |
|||
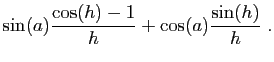 |
En utilisant les limites de la question précédente,
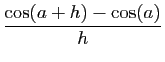 |
|||
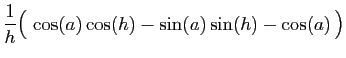 |
|||
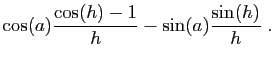 |
On en déduit :
![\begin{displaymath}
\begin{array}{rcl}
&\arcsin&\\
{[-1,1]}&\longrightarrow&[-\pi/2,\pi/2]\\
x&\longmapsto&\arcsin(x)
\end{array}\end{displaymath}](img271.gif)
![\begin{displaymath}
\begin{array}{rcl}
&\arccos&\\
{[-1,1]}&\longrightarrow&[0,\pi]\\
x&\longmapsto&\arccos(x)
\end{array}\end{displaymath}](img273.gif)
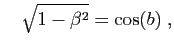
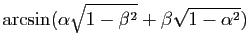 |
|||
Or :
![\begin{displaymath}
\arcsin(\sin(a+b))=\left\{
\begin{array}{lcl}
-\pi-(a+b)&\mb...
...2]\\
\pi-(a+b)&\mbox{si}&a+b\in[\pi/2,\pi]
\end{array}\right.
\end{displaymath}](img600.gif)
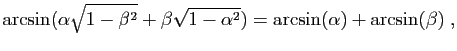
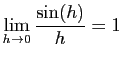 et
et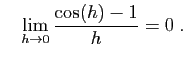
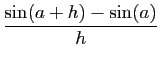 |
|||
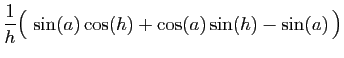 |
|||
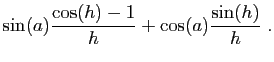 |
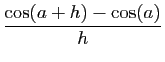 |
|||
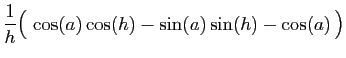 |
|||
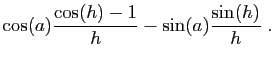 |
![\begin{displaymath}
\begin{array}{rcl}
&\arcsin&\\
{[-1,1]}&\longrightarrow&[-\pi/2,\pi/2]\\
x&\longmapsto&\arcsin(x)
\end{array}\end{displaymath}](img271.gif)
![\begin{displaymath}
\begin{array}{rcl}
&\arccos&\\
{[-1,1]}&\longrightarrow&[0,\pi]\\
x&\longmapsto&\arccos(x)
\end{array}\end{displaymath}](img273.gif)
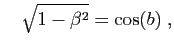
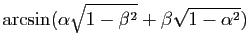 |
|||
![\begin{displaymath}
\arcsin(\sin(a+b))=\left\{
\begin{array}{lcl}
-\pi-(a+b)&\mb...
...2]\\
\pi-(a+b)&\mbox{si}&a+b\in[\pi/2,\pi]
\end{array}\right.
\end{displaymath}](img600.gif)
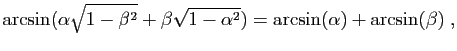
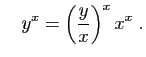
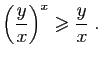
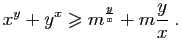
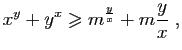
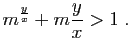
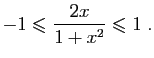
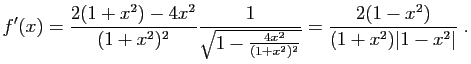
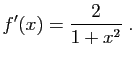
Sur les intervalles
![]() et
et
![]() ,
,
![]() , et
la dérivée de
, et
la dérivée de ![]() vaut
vaut
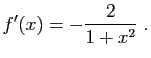
De même,
![]() et
et
![]() , donc
pour
, donc
pour
![]() ,
,
![]() .
.
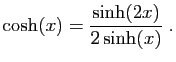
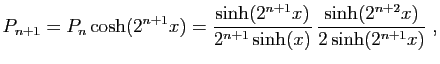
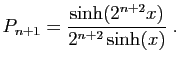
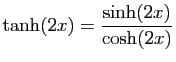
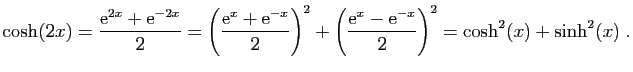
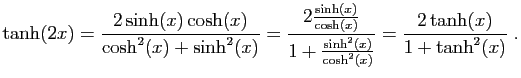
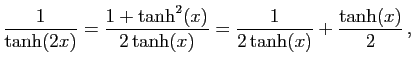
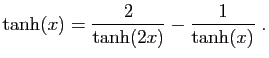
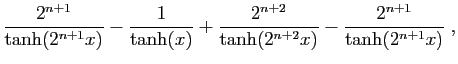 |
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales