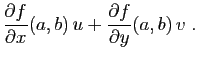
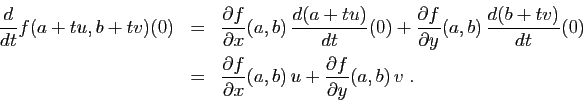
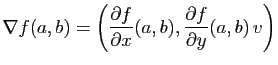 et
et
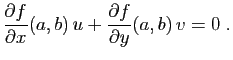
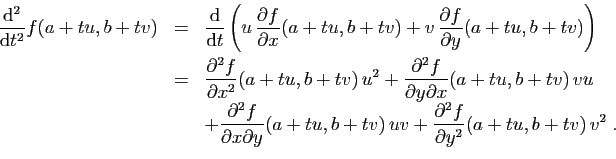
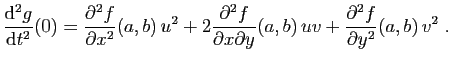
![\begin{displaymath}
(u,v)
\left(
\begin{array}{cc}
\frac{\partial^2 f}{\partial...
...ght)
\left(
\begin{array}{c}
u [2ex]
v
\end{array}\right)\;.
\end{displaymath}](img573.gif)
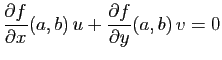
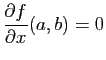 et
et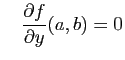
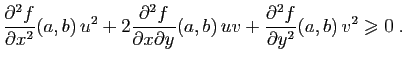
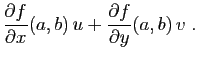
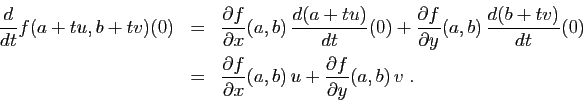
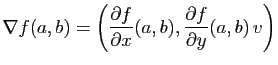 et
et
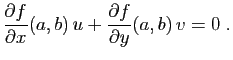
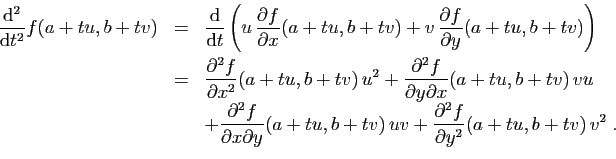
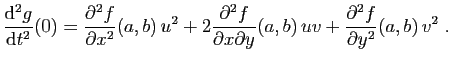
![\begin{displaymath}
(u,v)
\left(
\begin{array}{cc}
\frac{\partial^2 f}{\partial...
...ght)
\left(
\begin{array}{c}
u [2ex]
v
\end{array}\right)\;.
\end{displaymath}](img573.gif)
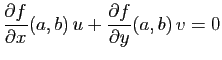
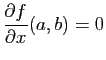 et
et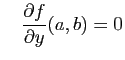
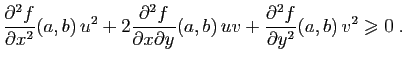
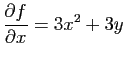 et
et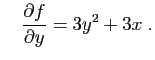
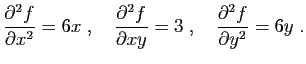
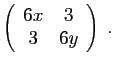
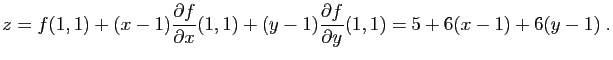
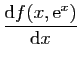 |
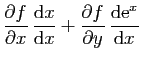 |
||
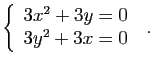
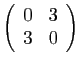 et
et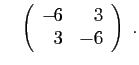
Les valeurs propres de la seconde matrice sont ![]() et
et ![]() .
Donc le point
.
Donc le point
![]() est un maximum
pour la surface d'équation
est un maximum
pour la surface d'équation ![]() .
.
![\begin{displaymath}
\left\{
\begin{array}{lcl}
u&=&\displaystyle{x+y} [2ex]
v&...
... [2ex]
y&=&\displaystyle{\frac{u-v}{2}}\;.
\end{array}\right.
\end{displaymath}](img605.gif)
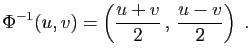
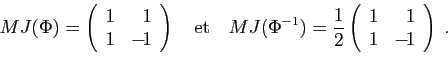
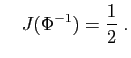
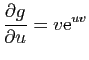 et
et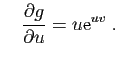
![\begin{displaymath}
\begin{array}{lcl}
\displaystyle{\frac{\partial g}{\partial ...
...x]
&=&(x+y)\mathrm{e}^{x^2-y^2}=u\mathrm{e}^{uv}\;,
\end{array}\end{displaymath}](img614.gif)
![\begin{displaymath}
\begin{array}{lcl}
\displaystyle{\frac{\partial g}{\partial ...
...x]
&=&(x-y)\mathrm{e}^{x^2-y^2}=v\mathrm{e}^{uv}\;,
\end{array}\end{displaymath}](img615.gif)
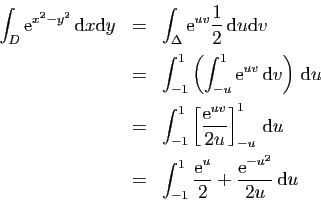
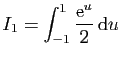 et
et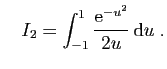
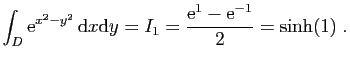
 |
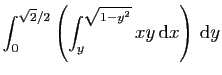 |
||
![$\displaystyle \int_0^{\sqrt{2}/2} \left[\frac{x^2y}{2}\right]_{y}^{\sqrt{1-y^2}} \mathrm{d}y$](img630.gif) |
|||
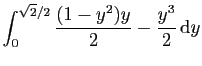 |
|||
![$\displaystyle \left[\frac{y^2}{4}-\frac{y^4}{4}\right]_0^{\sqrt{2}/2}$](img632.gif) |
|||
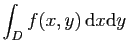 |
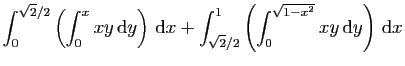 |
||
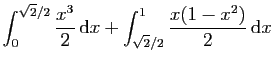 |
|||
![$\displaystyle \left[\frac{x^4}{8}\right]_0^{\sqrt{2}/2} +
\left[\frac{x^2}{4}-\frac{x^4}{8}\right]_{\sqrt{2}/2}^1$](img637.gif) |
|||
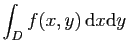 |
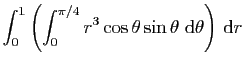 |
||
![$\displaystyle \left[\frac{r^4}{4}\right]_0^1\times
\left[\frac{-\cos 2\theta}{4}\right]_0^{\pi/4}$](img639.gif) |
|||
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales