Les intégrations successives peuvent conduire à des calculs
fastidieux si la fonction ou le domaine sont compliqués. La
technique du changement de variables permet de les simplifier.
Pour comprendre ce résultat, nous devons donner une interprétation
géométrique de l'intégrale et du jacobien.
Dans l'écriture
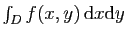 , il faut voir
, il faut voir
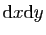 comme la surface d'un petit rectangle de largeur
comme la surface d'un petit rectangle de largeur
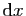 et de longueur
et de longueur
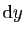 autour du point
autour du point 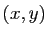 . Le produit
. Le produit
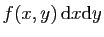 est le volume
d'un petit parallélépipède dont la base est ce rectangle et la
hauteur
est le volume
d'un petit parallélépipède dont la base est ce rectangle et la
hauteur 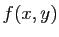 . L'intégrale est la somme de ces petits
éléments de volume (figure 11).
. L'intégrale est la somme de ces petits
éléments de volume (figure 11).
Figure 11:
Interprétation géométrique d'une intégrale double.
|
|
Appliquer le difféomorphisme 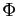 au domaine
au domaine 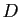 revient à le
déformer, comme si c'était une plaque de caoutchouc. Le petit
rectangle de largeur
revient à le
déformer, comme si c'était une plaque de caoutchouc. Le petit
rectangle de largeur
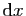 et de longueur
et de longueur
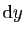 autour du point
autour du point 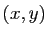 est lui aussi déformé en une petite surface, autour de
est lui aussi déformé en une petite surface, autour de
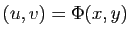 . En première approximation, cette petite surface
peut être vue comme un parallélogramme, dont l'aire
est
. En première approximation, cette petite surface
peut être vue comme un parallélogramme, dont l'aire
est
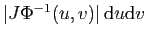 :
rappelons que le déterminant de deux vecteurs dans le plan est au
signe près l'aire du parallélogramme qu'ils délimitent
(cf. figure 12).
:
rappelons que le déterminant de deux vecteurs dans le plan est au
signe près l'aire du parallélogramme qu'ils délimitent
(cf. figure 12).
Figure:
Interprétation géométrique du terme
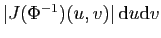 dans un changement de variables.
dans un changement de variables.
|
|
Soit à calculer
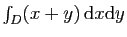 , où le domaine
, où le domaine 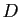 est
délimité par deux paraboles et deux hyperboles (figure
13).
est
délimité par deux paraboles et deux hyperboles (figure
13).
Figure 13:
Exemple de changement de variables.
|
|
On pourrait calculer directement cette intégrale de la façon
suivante.
Nous proposons le changement de variables suivant.
La première étape consiste à déterminer 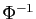 , en
résolvant en
, en
résolvant en 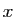 et
et 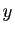 le système :
le système :
Ceci fournit l'expression explicite de 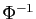 .
.
La seconde étape consiste à déterminer 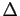 , qui est l'image
par
, qui est l'image
par 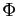 de
de 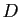 . Pour cela, on remplace
. Pour cela, on remplace 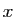 et
et 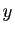 par leurs
expressions en fonction de
par leurs
expressions en fonction de 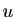 et
et 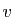 dans les inégalités
définissant
dans les inégalités
définissant 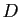 .
.
La troisième étape consiste à calculer le déterminant jacobien
de 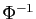 . Pour cela, il faut d'abord écrire la matrice
jacobienne, en dérivant les expressions de
. Pour cela, il faut d'abord écrire la matrice
jacobienne, en dérivant les expressions de 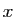 et
et 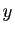 en fonction de
en fonction de
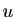 et
et 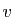 .
.
La quatrième étape consiste à appliquer le théorème
9. Pour cela, on remplace 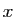 et
et 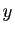 par leurs
expressions en fonction de
par leurs
expressions en fonction de 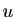 et
et 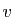 dans la fonction, et on
multiplie par la valeur absolue du jacobien.
Il ne reste plus qu'à calculer cette nouvelle intégrale.
dans la fonction, et on
multiplie par la valeur absolue du jacobien.
Il ne reste plus qu'à calculer cette nouvelle intégrale.
Le changement de variables en coordonnées polaires s'impose quand
le domaine 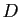 est un disque centré en 0.
Soit à calculer
est un disque centré en 0.
Soit à calculer
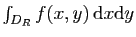 , où :
, où :
Le changement en coordonnées polaires envoie le disque 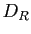 ,
privé du segment joignant l'origine à
,
privé du segment joignant l'origine à 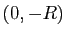 , sur un
domaine rectangulaire :
, sur un
domaine rectangulaire :
Le jacobien de 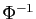 , déjà calculé, vaut
, déjà calculé, vaut 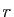 . On a donc :
. On a donc :
Calculons le volume de la boule de rayon
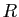 ,
à l'aide du changement de variables en coordonnées sphériques.
,
à l'aide du changement de variables en coordonnées sphériques.
Le difféomorphisme 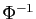 est :
est :
Nous avons déjà écrit sa matrice jacobienne, et nous laissons
au lecteur le calcul de son déterminant :
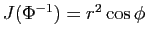 .
.
Le volume de la boule 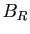 est :
est :
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
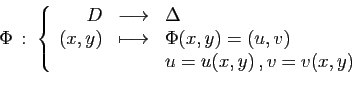
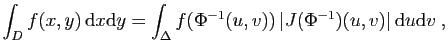
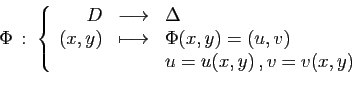
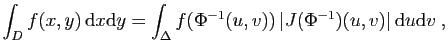
![]() au domaine
au domaine ![]() revient à le
déformer, comme si c'était une plaque de caoutchouc. Le petit
rectangle de largeur
revient à le
déformer, comme si c'était une plaque de caoutchouc. Le petit
rectangle de largeur
![]() et de longueur
et de longueur
![]() autour du point
autour du point ![]() est lui aussi déformé en une petite surface, autour de
est lui aussi déformé en une petite surface, autour de
![]() . En première approximation, cette petite surface
peut être vue comme un parallélogramme, dont l'aire
est
. En première approximation, cette petite surface
peut être vue comme un parallélogramme, dont l'aire
est
![]() :
rappelons que le déterminant de deux vecteurs dans le plan est au
signe près l'aire du parallélogramme qu'ils délimitent
(cf. figure 12).
:
rappelons que le déterminant de deux vecteurs dans le plan est au
signe près l'aire du parallélogramme qu'ils délimitent
(cf. figure 12).
![]() , où le domaine
, où le domaine ![]() est
délimité par deux paraboles et deux hyperboles (figure
13).
est
délimité par deux paraboles et deux hyperboles (figure
13).
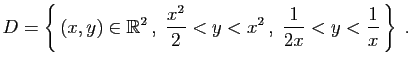
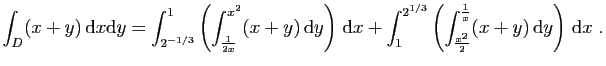
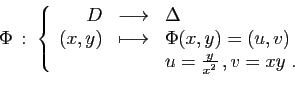
![\begin{displaymath}
\left\{
\begin{array}{rcl}
u&=& \displaystyle{\frac{y}{x^2}}...
...-1/3}v^{1/3} [1ex]
y&=& u^{1/3}v^{2/3}\;.
\end{array}\right.
\end{displaymath}](img324.gif)
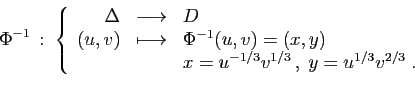
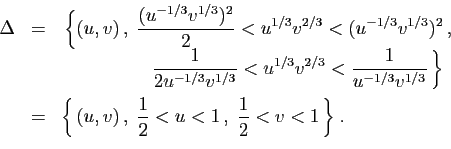
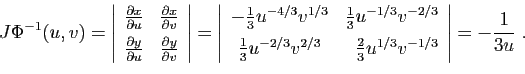
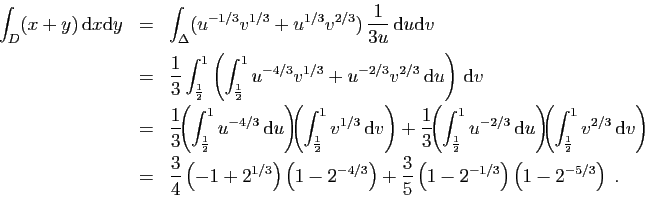
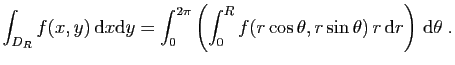
![\begin{displaymath}
\begin{array}{rcl}
]0,R[\times ]0,2\pi[\times ]-\frac{\pi}{2...
...os\theta ,\;y=r\cos\phi\sin\theta
,\;z=r\sin\phi
\end{array}\end{displaymath}](img339.gif)
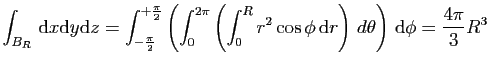
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales