Fonction zéta et nombres premiers

La «fonction zéta de Riemann» nous vient en fait d'Euler. Il s'agit de la fonction qui à un exposant $s$ associe :

$$\zeta(s) = \sum_{n=1}^{+\infty} \frac{1}{n^s}\;.$$

La détermination de $\zeta(2)=\frac{\pi^2}{6}$, puis dans la foulée de $\zeta(2n)$ pour $n\in\mathbb{N}^*$ est un des exploits dont Euler était le plus fier. Il ne s'était pas arrêté là. Il avait aussi compris le rapport des séries de ce type avec les nombres premiers. Voici la traduction du théorème 7 de «Variae observationes circa series infinitas» paru aux commentaires de l'Académie des Sciences de Saint-Pétersbourg en 1744 (le travail date de 1737).

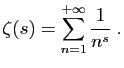
THÉORÈME 7. Si nous poussons jusqu'à l'infini la continuation des fractions

$$\frac{2\cdot 3\cdot 5\cdot 7\cdot 11\cdot 13\cdot 17\cdot 19\cdots}{1\cdot 2\cdot 4\cdot 6\cdot 10\cdot 12\cdot 16\cdot 18\cdots}$$

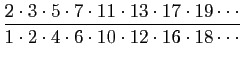
dont les numérateurs sont tous les entiers premiers et les dénominateurs sont les mêmes moins une unité, le résultat est le même que la somme de la série

$$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\cdots$$

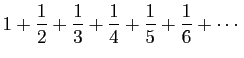
qui est certainement infinie.

La «démonstration» est un concentré d'audace eulérienne.

DÉMONSTRATION : Si nous avons

$$x=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\cdots\;,$$

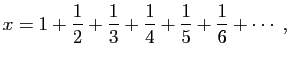
alors nous aurons

$$\frac{1}{2}x=\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+\cdots\;,$$

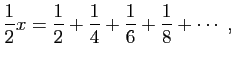
qui soustraite de la première nous donnera

$$\frac{1}{2}x=1+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\cdots\;,$$

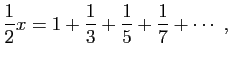
série où aucun dénominateur n'est pair. De celle-là, nous soustrayons encore la série suivante

$$\frac{1}{2}\cdot \frac{1}{3} x= \frac{1}{3}+\frac{1}{9}+\frac{1}{15}+ \frac{1}{21}+\cdots\;;$$

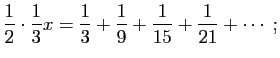
et nous aurons

$$\frac{1}{2}\cdot\frac{2}{3} x = 1+\frac{1}{5}+ \frac{1}{7}+ \frac{1}{11}+\frac{1}{13}+\cdots\;,$$

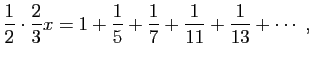
où parmi les dénominateurs nous n'en trouvons aucun divisible soit par $2$ soit par $3$. Afin d'ôter les nombres divisibles par $5$, nous soustrayons la série suivante.

$$\frac{1\cdot 2}{2\cdot 3}\cdot\frac{1}{5} x = \frac{1}{5}+\frac{1}{25}+ \frac{1}{35}+\cdots$$

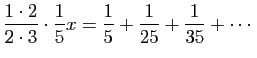
et nous aurons

$$\frac{1\cdot 2\cdot 4}{2\cdot 3\cdot 5} x =1+\frac{1}{7}+\frac{1}{11}+\frac{1}{13}+\cdots\;.$$

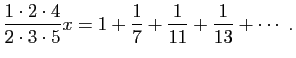
Et procédant de la même manière, soustrayant tous les termes divisibles d'abord par $7$, puis par $11$, puis par tous les nombres premiers, nous aurons finalement

$$\frac{1\cdot 2\cdot 4\cdot 6\cdot 10\cdot 12\cdot 16\cdot 18\cdot... ...\cdot 3\cdot 5\cdot 7\cdot 11\cdot 13\cdot 17\cdot 19\cdot 23\cdots} x=1\;.$$

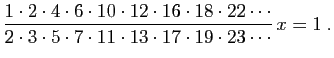
Puisque

$$x=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\cdots\;,$$

nous avons

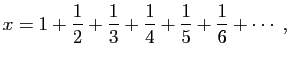
$$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\fr... ...dots}{1\cdot 2\cdot 4\cdot 6\cdot 10\cdot 12\cdot 16\cdot 18\cdot 22\cdots}\;,$$

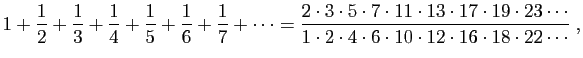
expression dont les numérateurs constituent la suite des nombres premiers et les dénominateurs sont les mêmes moins une unité. Q. E. D.

Dans le théorème 8 Euler généralise avec le même type d'argument, mais cette fois ci les valeurs sont finies.

THÉORÈME 8. L'expression formée à partir de la suite des nombres premiers

$$\frac{2^n\quad\cdot\quad 3^n\quad \cdot\quad 5^n\quad \cdot\quad ... ...\quad \cdot\quad 11^n\quad\cdots} {(2^n-1)(3^n-1)(5^n-1)(7^n-1)(11^n-1)\cdots}$$

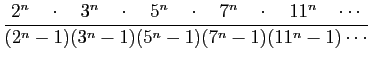
a la même valeur que la somme de la série

$$1+\frac{1}{2^n}+\frac{1}{3^n}+\frac{1}{4^n}+\frac{1}{5^n}+ \frac{1}{6^n}+\frac{1}{7^n}+\cdots$$

Bon, assez ri ! Vous n'êtes pas Euler, et vous en savez assez pour démontrer rigoureusement le résultat suivant.

Théorème 28   Soit $D=\{ z\in\mathbb{C} ,\; \mathrm{Re}(z)>1\}$. La fonction qui à $s\in D$ associe

$$\zeta(s) = \sum_{n=1}^{+\infty} \frac{1}{n^s}$$

est holomorphe sur $D$. Soit $\mathbb{P}$ l'ensemble des entiers premiers. Pour tout $s\in D$, le produit

$$\prod_{p\in\mathbb{P}} \frac{1}{1-\frac{1}{p^s}}$$

est convergent et égal à $\zeta(s)$.

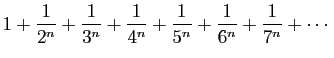
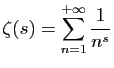
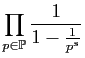
Au fait, pourquoi Euler avait-il commencé dans son mémoire par le cas $n=1$ ? Les corollaires de son théorème 7 montrent ce qu'il avait derrière la tête.

COROLLAIRE 1. Ainsi la valeur de l'expression

$$\frac{2\cdot 3 \cdot 5\cdot 7\cdot 11 \cdot 13 \ldots} {1\cdot 2 \cdot 4\cdot 6\cdot 10 \cdot 12 \ldots}$$

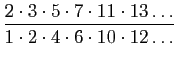
est infinie et si nous notons l'infinité absolue $\infty$, la valeur de cette expression est $l\infty$ qui est le minimum parmi toutes les puissances de l'infini.

(Euler veut parler de $\ln(+\infty)$, vous l'aurez compris !) Dans la foulée, il revisite le théorème d'Euclide.

COROLLAIRE 2. Comme l'expression

$$\frac{4\cdot 9 \cdot 16\cdot 25\cdot 36 \cdot 49 \cdots} {3\cdot 8 \cdot 15\cdot 24\cdot 35 \cdot 48 \cdots}$$

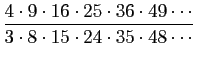
a une valeur finie qui est $2$, il s'ensuit que les nombres premiers sont infiniment plus nombreux que les carrés dans la suite de tous les nombres.

D'accord, il y a une infinité de nombres premiers, mais quelle infinité ?

COROLLAIRE 3. Également à partir de là, il est également vrai que les nombres premiers sont infiniment moins nombreux que les nombres entiers, puisque l'expression

$$\frac{2\cdot 3\cdot 4\cdot 5\cdot 6\cdot 7\cdots} {1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6\cdots}$$

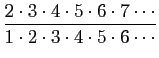
est infinie, et que la valeur analogue pour des nombres premiers est le logarithme de cette valeur.

Comparez avec son théorème 19.

THÉORÈME 19. La somme des réciproques des nombres premiers,

$$\frac{1}{2}+\frac{1}{3}+\frac{1}{5}+ \frac{1}{7}+\frac{1}{11}+\frac{1}{13}+\cdots$$

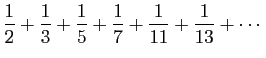
est infinie, mais elle est infiniment moindre que la somme de la série harmonique

$$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\cdots$$

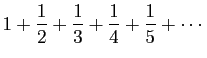
car la première est comme le logarithme de la seconde.

Le «théorème de raréfaction des nombres premiers», pressenti par Euler, n'a été correctement conjecturé (par Gauss et Legendre) qu'à la fin du XVIII^e, et démontré rigoureusement (par Hadamard et de la Vallée Poussin) qu'à la fin du XIX^e.

Théorème 29   Pour tout $x\in \mathbb{R}^+$, soit $\pi(x)$ le cardinal de l'ensemble des nombres premiers inférieurs à $x$.

$$\lim_{x\to \infty} \frac{\pi(x)}{x/\ln(x)}=1\;.$$

Entre les deux, un petit mémoire de 8 pages, présenté par Bernhard Riemann (1826-1866) pour son admission comme correspondant à l'Académie de Berlin en 1859, avait révolutionné la question, et donné du grain à moudre aux générations suivantes : «Sur le nombre des nombres premiers inférieurs à une grandeur donnée». L'idée de génie de Riemann était d'avoir prolongé la fonction zéta en une fonction méromorphe dans tous le plan complexe, avec un pôle unique en $1$, et d'avoir donné une formule exacte reliant $\pi(x)$ aux zéros de la fonction zéta ainsi prolongée⁷. Dans le cours de sa démonstration, il était amené à utiliser le fait que les zéros de la fonction zéta, autres que les entiers négatifs pairs, sont tous de partie réelle égale à $\frac{1}{2}$ ; et Riemann d'ajouter incidemment :

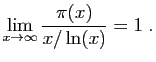
Il serait à désirer, sans doute, que l'on eût une démonstration rigoureuse de cette proposition ; néanmoins j'ai laissé cette recherche de côté pour le moment après quelques rapides essais infructueux, car elle paraît superflue dans le but de notre étude.

En 2004 Gourdon et Demichel ont calculé dix mille milliards de zéros de la fonction zéta ; ils sont tous de partie réelle $\frac{1}{2}$. Personne ne doute vraiment que l'«hypothèse de Riemann» soit exacte, mais elle n'est toujours pas démontrée. André Weil (1906-1998) a dit :

Quand j'étais jeune, j'espérais démontrer l'hypothèse de Riemann. Quand je suis devenu un peu plus vieux, j'ai encore eu l'espoir de pouvoir lire et comprendre une démonstration de l'hypothèse de Riemann. Maintenant, je me contenterais bien d'apprendre qu'il en existe une démonstration.

Le problème est inclus dans la liste des «problèmes du millénaire» et une prime d'un million de dollars est offert à celui qui trouvera la solution. Alors vous qui êtes jeunes...