Le calcul des résidus

Ne croyez pas qu'une théorie comme celle des fonctions d'une variable complexe sorte un beau jour de la tête d'un mathématicien sous sa forme définitive. Elle est l'aboutissement d'un long processus de maturation, qui se nourrit le plus souvent des tâtonnements et des échanges de plusieurs contributeurs. De 1814 jusqu'aux années 1840 où commencent à émerger les hypothèses les plus générales, en passant par son monumental «Mémoire de Turin» de 1831, Cauchy élabore quasiment seul sa théorie des fonctions d'une variable complexe. Elle émerge au fil de nombreux « Mémoires sur les intégrales définies» dont il est intéressant de suivre le fil tout au long des années. L'adhésion de ses collègues est loin d'être immédiate. Voici ce qu'écrit Denis Poisson à propos du mémoire de 1814.

[...] il semble que l'équation (1) et celles qui s'en déduisent devraient déterminer quelques intégrales nouvelles ; mais parmi les nombreux exemples que l'auteur a rassemblés dans la première partie de son Mémoire, je n'ai remarqué aucune intégrale qui ne fût pas déjà connue, ce qui tient sans doute à ce que son procédé, quoique très général et très uniforme, n'est pas essentiellement distinct de ceux qu'on a employés jusqu'ici.

[...]

Ce que le mémoire dont nous rendons compte contient, selon nous, de plus curieux, c'est l'usage que l'auteur fait des intégrales qu'il nomme singulières, pour exprimer d'autres intégrales prises entre des limites finies. Il parvient ainsi à plusieurs résultats déjà connus. Cette manière indirecte de les obtenir ne doit pas être préférée aux méthodes ordinaires, mais elle n'est pas moins très remarquable, et digne de l'attention des géomètres.

Le moins qu'on puisse dire est que Poisson ne fait pas preuve d'un enthousiasme excessif pour saluer la naissance de la méthode des résidus. Il faut dire qu'elle n'en était qu'à ses balbutiements : il ne s'agissait encore pour Cauchy que d'exprimer que l'intégrale d'une fonction sur le bord d'un rectangle du plan complexe est nulle, sous des conditions encore assez peu claires, mais qui allaient s'affiner au fil des mémoires suivants. Peut-être Cauchy pensait-il au rapport mitigé de Poisson, en écrivant son «Mémoire sur les intégrales définies où l'on donne une formule générale de laquelle se déduisent les valeurs de la plupart des intégrales définies déjà connues et celles d'un grand nombre d'autres». Il est publié aux Annales de Mathématiques en deux parties ; la seconde, datée de 1826 et consacrée aux applications, contient rien moins que 190 formules intégrales obtenues par la méthode des résidus ! Êtes-vous curieux de savoir à quoi ressemblait la théorème des résidus à sa naissance ? Le voici énoncé en 1822 dans le «Mémoire sur les intégrales définies où l'on fixe le nombre et la nature des constantes arbitraires que peuvent comporter les valeurs de ces mêmes intégrales quand elles deviennent indéterminées».

Si l'on désigne par $x_0, x_1, \ldots, x_{n-1}$ les racines de l'équation

$$\frac{1}{f(x)}=0\;,$$

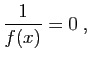
dans lesquelles les parties réelles restent comprises entre les limites $x'$, $x''$, et les coefficients de $\sqrt{-1}$ entre les limites $y'$, $y''$, et par $f_0, f_1, \ldots, f_{n-1}$ les véritables valeurs des produits $kf(x_0+k), kf(x_1+k), \ldots, kf(x_{n-1}+k)$, correspondantes à $k=0$, on aura

$$\displaystyle{\int_{x'}^{x''} \left[f(x+y'\sqrt{-1}]- f(x+y''\sqrt{-1})\right] \mathrm{d}x}$$

$$\hspace*{1cm}=\sqrt{-1} \displaystyle{\int_{y'}^{y''} \left[f(x'+y\sqrt{-1}]- f(x''+y\sqrt{-1})\right] \mathrm{d}y}$$

$$\hspace*{2cm}-2\pi\sqrt{-1} \left( f_0+f_1+\cdots+f_{n-1}\right)\;.$$

Et maintenant à vous de jouer !

1. Quelle définition Cauchy donne-t-il des pôles ?
2. Comment définiriez-vous rigoureusement les «valeurs véritables des produits...»
3. De quel théorème du cours l'énoncé de Cauchy est-il un cas particulier ?
4. Sur quel chemin fermé de classe $\mathcal {C}^1$ par morceaux, l'intégrale est-elle prise ?
5. Comment l'énoncé de Cauchy s'écrirait-il en notations modernes ?