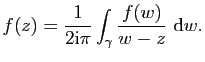
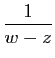 |
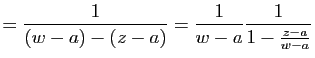 |
|
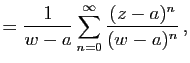 |
d'où
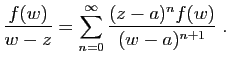
Cette série de fonctions de ![]() est normalement convergente donc
uniformément convergente sur le cercle
est normalement convergente donc
uniformément convergente sur le cercle
![]() puisque son terme général est
majoré par
puisque son terme général est
majoré par
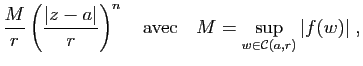
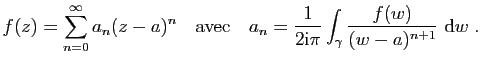
La
fonction ![]() est donc développable en série entière sur le disque
est donc développable en série entière sur le disque
![]() et par conséquent analytique dans
et par conséquent analytique dans ![]() .
.
Si ![]() est une fonction holomorphe dans le disque de centre
est une fonction holomorphe dans le disque de centre ![]() et
de rayon
et
de rayon ![]() , pour tout
, pour tout ![]() et
et
![]() on a, si
on a, si
![]() ,
,
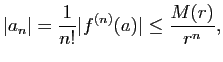
Cette inégalité se démontre ainsi.
D'après le 1) et le 2) la fonction ![]() est développable en série entière dans le disque
est développable en série entière dans le disque ![]() et on a pour tout
et on a pour tout ![]() tel que
tel que ![]() ,
,
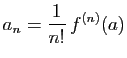 |
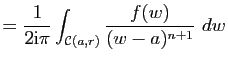 |
|
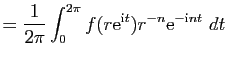 |
Si on pose
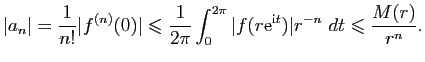
Si ![]() est une fonction holomorphe dans
est une fonction holomorphe dans
![]() tout entier et
si
tout entier et
si ![]() est bornée, alors
est bornée, alors ![]() est constante.
est constante.
Ce théorème se démontre ainsi.
Puisque ![]() est holomorphe dans
est holomorphe dans
![]() et bornée, il
existe
et bornée, il
existe ![]() tel que
tel que
![]() pour tout
pour tout
![]() et les
inégalités de Cauchy donnent alors
et les
inégalités de Cauchy donnent alors
![]() pour tout
pour tout ![]() et tout
et tout
![]() , ce qui implique
, ce qui implique
![]() , si
, si
![]() .
.
Montrons par contraposée que tout polynôme à coefficients complexes
non constant possède au moins une racine.
Soit
![]() un polynôme de degré
strictement supérieur à
un polynôme de degré
strictement supérieur à ![]() , supposons que
, supposons que ![]() n'admet pas de racine
dans
n'admet pas de racine
dans
![]() . La fonction
. La fonction
![]() est alors holomorphe
dans
est alors holomorphe
dans
![]() et bornée
puisque
et bornée
puisque
![]() quand
quand
![]() , elle est donc
constante par le Théorème de Liouville.
, elle est donc
constante par le Théorème de Liouville.
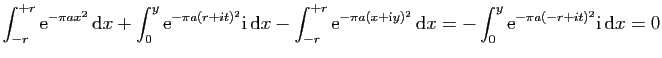
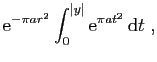
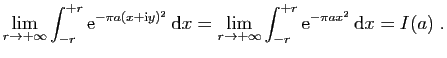
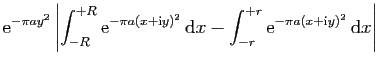

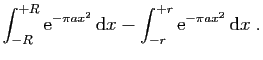
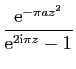
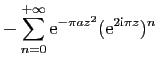
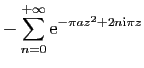
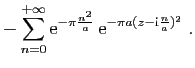
![$\displaystyle \displaystyle{
\int_{[-r+\mathrm{i},r+\mathrm{i}]} f(z) \mathrm{d}z}$](img1567.gif)
![$\displaystyle \displaystyle{
-\sum_{n=0}^{+\infty}\mathrm{e}^{-\pi \frac{n^2}{a...
...{i},r+\mathrm{i}]}
\mathrm{e}^{-\pi a(z-\mathrm{i}\frac{n}{a})^2} \mathrm{d}z}$](img1568.gif)
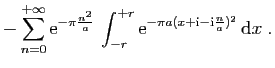
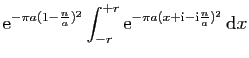
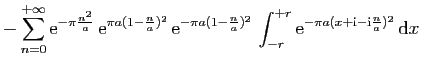
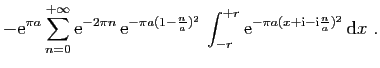
![$\displaystyle \displaystyle{
\lim_{r\to+\infty}\int_{[-r+\mathrm{i},r+\mathrm{i}]} f(z) \mathrm{d}z}$](img1574.gif)
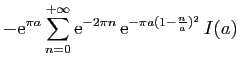
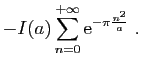
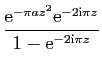
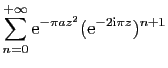
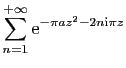
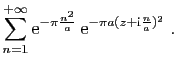
![$\displaystyle \displaystyle{
\int_{[-r-\mathrm{i},r-\mathrm{i}]} f(z) \mathrm{d}z}$](img1585.gif)
![$\displaystyle \displaystyle{
\sum_{n=1}^{+\infty}\mathrm{e}^{-\pi \frac{n^2}{a}...
...{i},r-\mathrm{i}]}
\mathrm{e}^{-\pi a(z+\mathrm{i}\frac{n}{a})^2} \mathrm{d}z}$](img1586.gif)
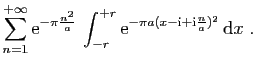
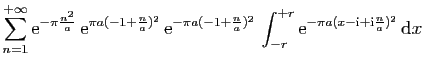
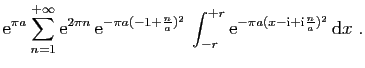
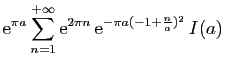
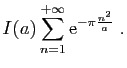
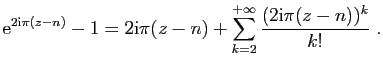
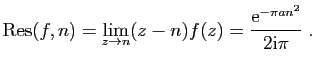
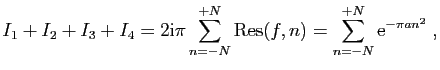
![$\displaystyle I_1=\int_{[-N-\frac{1}{2}-\mathrm{i},N+\frac{1}{2}-\mathrm{i}]}f(...
...\int_{[N+\frac{1}{2}-\mathrm{i},N+\frac{1}{2}+\mathrm{i}]}f(z) \mathrm{d}z\;,
$](img1596.gif)
![$\displaystyle I_3=\int_{[N+\frac{1}{2}+\mathrm{i},-N-\frac{1}{2}+\mathrm{i}]}f(...
...t_{[-N-\frac{1}{2}+\mathrm{i},-N-\frac{1}{2}-\mathrm{i}]}f(z) \mathrm{d}z
\;.
$](img1597.gif)
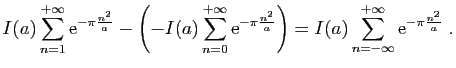
![$\displaystyle \displaystyle{
\left\vert\int_{[N+\frac{1}{2}-\mathrm{i},N+\frac{1}{2}+\mathrm{i}]}f(z) \mathrm{d}
z\right\vert}$](img1603.gif)
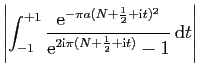
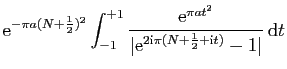
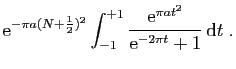
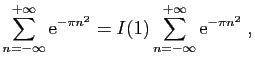
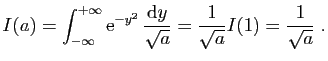
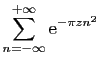 et
et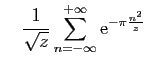
![$\displaystyle \Gamma(z+1) = \int_0^{+\infty}t^z\mathrm{e}^{-t} \mathrm{d}t
=
\...
...}\right]_0^{+\infty} +\int_0^{+\infty}
zt^{z-1}\mathrm{e}^{-t} \mathrm{d}t\;.
$](img1624.gif)
![$\displaystyle \Gamma(1) = \int_0^{+\infty}t^0\mathrm{e}^{-t} \mathrm{d}t =
\left[-\mathrm{e}^{-t}\right]_0^{+\infty} = 1\;.
$](img1628.gif)
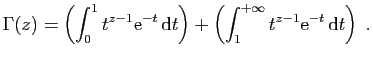
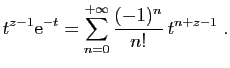
![$\displaystyle \forall t\in [0,1]\;,\quad
\left\vert\frac{(-1)^n}{n!} t^{n+z-1}\right\vert\leqslant \frac{1}{n!}\;.
$](img1632.gif)
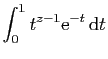
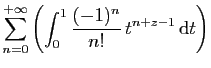
![$\displaystyle \displaystyle{
\sum_{n=0}^{+\infty}
\frac{(-1)^n}{n!}\left[\frac{t^{n+z}}{n+z}\right]_0^1}$](img1635.gif)
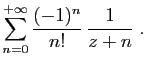
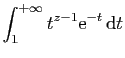
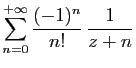
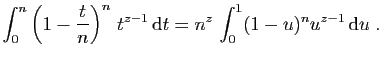
![$\displaystyle I_n(z)= \left[(1-u)^n\frac{u^z}{z}\right]_0^1 +
\frac{n}{z} \int_0^1 (1-u)^{n-1} u^z \mathrm{d}u
=
\frac{n}{z}I_{n-1}(z+1)\;.
$](img1647.gif)
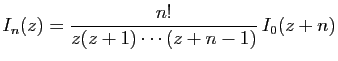
![$\displaystyle I_0(z+n)= \int_0^1 t^{z+n-1} \mathrm{d}t
=
\left[\frac{t^{z+n}}{z+n}\right]_0^1
=
\frac{1}{z+n}\;.
$](img1649.gif)
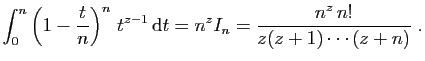
![$\displaystyle \left\vert\left(1-\frac{t}{n}\right)^nt^{z-1} \mathbb{I}_{[0,n]}(t)\right\vert
\leqslant \mathrm{e}^{-t}t^{\mathrm{Re} z-1}\;,
$](img1656.gif)
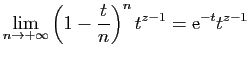
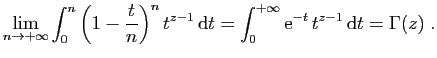
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales