D'après le théorème 3,
un sous-espace vectoriel contient toutes les combinaisons
linéaires d'un nombre quelconque de vecteurs : pour tout entier 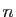 ,
pour tous vecteurs
,
pour tous vecteurs
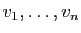 de
de  , et pour tous réels
, et pour tous réels
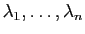 ,
,
Une des manières de fabriquer un sous-espace vectoriel est de partir
d'une famille d'éléments, puis de lui adjoindre toutes les
combinaisons linéaires de ces éléments. Une famille
d'éléments de  est définie comme une application d'un
ensemble d'indices
est définie comme une application d'un
ensemble d'indices 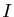 , à valeurs dans
, à valeurs dans  .
.
L'ensemble des combinaisons linéaires
d'éléments de 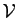 est un espace vectoriel, d'après le
théorème 3. Le même théorème implique
aussi que tout espace vectoriel contenant
est un espace vectoriel, d'après le
théorème 3. Le même théorème implique
aussi que tout espace vectoriel contenant 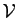 doit contenir
toutes les combinaisons linéaires de ses éléments. Donc le
sous-espace engendré par
doit contenir
toutes les combinaisons linéaires de ses éléments. Donc le
sous-espace engendré par 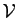 est inclus dans tout sous-espace
contenant
est inclus dans tout sous-espace
contenant 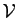 .
Voici quelques exemples de familles avec les espaces qu'elles
engendrent.
.
Voici quelques exemples de familles avec les espaces qu'elles
engendrent.
| Complexes |
| Famille |
Espace engendré |
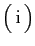 |
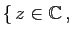 Re Re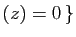 |
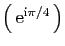 |
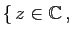 Re Re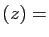 Im Im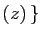 |
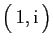 |
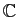 |
| Couples de réels |
| Famille |
Espace engendré |
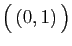 |
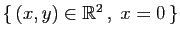 |
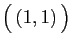 |
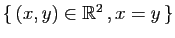 |
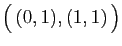 |
 |
| Matrices |
| Famille |
Espace engendré |
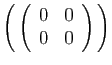 |
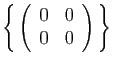 |
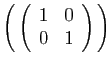 |
 |
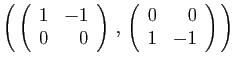 |
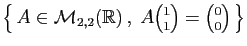 |
| Suites de réels |
| Famille |
Espace engendré |
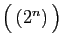 |
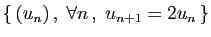 |
 |
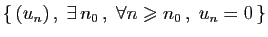 |
![$ \big( (u_n) ,\;\forall n ,\;u_n\in[0,1] \big)$](img171.gif) |
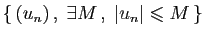 |
| Polynômes |
| Famille |
Espace engendré |
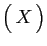 |
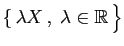 |
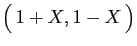 |
![$ \{ P\in\mathbb{R}[X] ,\;$](img118.gif) deg deg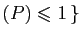 |
![$ \big( P\in\mathbb{R}[X] ,\;P(1)=1 \big)$](img177.gif) |
![$ \mathbb{R}[X]$](img178.gif) |
Fonctions de
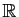 dans dans
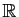 |
| Famille |
Espace engendré |
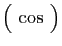 |
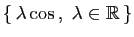 |
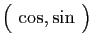 |
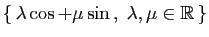 |
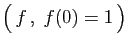 |
 |
Notre définition de la somme de deux sous-espaces utilise la
notion de sous-espace engendré.
La justification du terme «somme» et l'intérêt de cette notion
résident dans la proposition suivante.
Proposition 4
Soient  un espace vectoriel,
un espace vectoriel,  et
et  deux sous-espaces
vectoriels de
deux sous-espaces
vectoriels de  .
.
-
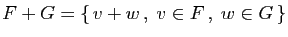 .
.
- Si
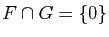 , alors pour tout vecteur
, alors pour tout vecteur 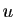 dans
dans 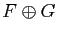 il
existe un unique couple de vecteurs
il
existe un unique couple de vecteurs 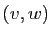 , tels que
, tels que 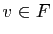 ,
, 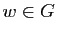 et
et 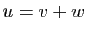 .
.
La figure 1 illustre la notion de somme directe.
Figure 1:
Somme directe d'espaces vectoriels et décomposition d'un
vecteur de la somme.
|
|
Démonstration : Tout vecteur de la forme 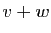 , où
, où 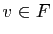 et
et 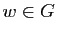 , appartient
à l'espace engendré par
, appartient
à l'espace engendré par 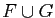 . Réciproquement l'espace
engendré par
. Réciproquement l'espace
engendré par 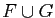 est formé des combinaisons
linéaires d'un nombre quelconque
d'éléments de
est formé des combinaisons
linéaires d'un nombre quelconque
d'éléments de 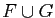 . Mais une telle combinaison
linéaire peut s'écrire comme la somme de deux combinaisons
linéaires : l'une ne contient que des éléments de
. Mais une telle combinaison
linéaire peut s'écrire comme la somme de deux combinaisons
linéaires : l'une ne contient que des éléments de  , et
appartient donc à
, et
appartient donc à  , l'autre ne contient que des éléments de
, l'autre ne contient que des éléments de  , et
appartient donc à
, et
appartient donc à  .
.
Dans le cas où la somme est directe, l'existence de la
décomposition 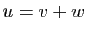 est démontrée par ce qui
précède. Nous devons prouver l'unicité.
Supposons
est démontrée par ce qui
précède. Nous devons prouver l'unicité.
Supposons
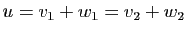 , avec
, avec
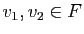 et
et
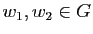 . Les deux vecteurs
. Les deux vecteurs 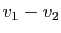 et
et 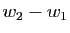 sont égaux, donc ils
appartiennent
à la fois à
sont égaux, donc ils
appartiennent
à la fois à  et à
et à  .
Par hypothèse,
.
Par hypothèse,
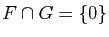 ,
donc
,
donc 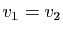 et
et 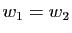 .
.  Dans l'espace vectoriel
Dans l'espace vectoriel
![$ \mathbb{R}[X]$](img178.gif) des polynômes, considérons les
deux familles suivantes :
des polynômes, considérons les
deux familles suivantes :
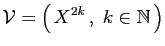
et
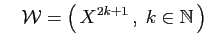
Ce sont respectivement les familles des monômes de degrés pairs,
et des monômes de degré impair. Soient  et
et  les espaces
vectoriels engendrés respectivement par
les espaces
vectoriels engendrés respectivement par 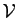 et
et 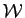 . L'espace vectoriel
. L'espace vectoriel  contient
tous les polynômes constitués
uniquement de monômes de degrés pairs : par exemple,
contient
tous les polynômes constitués
uniquement de monômes de degrés pairs : par exemple,
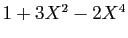 . L'espace vectoriel
. L'espace vectoriel  contient le polynôme nul, et
tous les polynômes constitués
uniquement de monômes de degrés impairs : par exemple,
contient le polynôme nul, et
tous les polynômes constitués
uniquement de monômes de degrés impairs : par exemple,
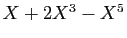 . L'intersection de
. L'intersection de  et
et  est réduite au
polynôme nul. De plus, tout polynôme de
est réduite au
polynôme nul. De plus, tout polynôme de
![$ \mathbb{R}[X]$](img178.gif) s'écrit (de
façon unique) comme somme d'un élément de
s'écrit (de
façon unique) comme somme d'un élément de  et d'un
élément de
et d'un
élément de  . Par exemple :
. Par exemple :
Les sous-espaces  et
et  sont supplémentaires dans
sont supplémentaires dans
![$ \mathbb{R}[X]$](img178.gif) .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
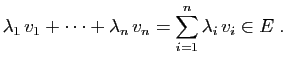
![]() est une famille génératrice pour
est une famille génératrice pour ![]() si le sous-espace engendré par
si le sous-espace engendré par ![]() est
est ![]() lui-même.
lui-même.
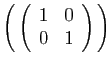

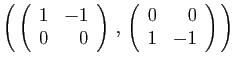
![]() , on dit que la somme est directe, et on la note
, on dit que la somme est directe, et on la note
![]() .
.
![]() , on dit que
, on dit que ![]() et
et ![]() sont supplémentaires dans
sont supplémentaires dans ![]() .
.![]() , où
, où ![]() et
et ![]() , appartient
à l'espace engendré par
, appartient
à l'espace engendré par ![]() . Réciproquement l'espace
engendré par
. Réciproquement l'espace
engendré par ![]() est formé des combinaisons
linéaires d'un nombre quelconque
d'éléments de
est formé des combinaisons
linéaires d'un nombre quelconque
d'éléments de ![]() . Mais une telle combinaison
linéaire peut s'écrire comme la somme de deux combinaisons
linéaires : l'une ne contient que des éléments de
. Mais une telle combinaison
linéaire peut s'écrire comme la somme de deux combinaisons
linéaires : l'une ne contient que des éléments de ![]() , et
appartient donc à
, et
appartient donc à ![]() , l'autre ne contient que des éléments de
, l'autre ne contient que des éléments de ![]() , et
appartient donc à
, et
appartient donc à ![]() .
.
![]() est démontrée par ce qui
précède. Nous devons prouver l'unicité.
Supposons
est démontrée par ce qui
précède. Nous devons prouver l'unicité.
Supposons
![]() , avec
, avec
![]() et
et
![]() . Les deux vecteurs
. Les deux vecteurs ![]() et
et ![]() sont égaux, donc ils
appartiennent
à la fois à
sont égaux, donc ils
appartiennent
à la fois à ![]() et à
et à ![]() .
Par hypothèse,
.
Par hypothèse,
![]() ,
donc
,
donc ![]() et
et ![]() .
. ![]() Dans l'espace vectoriel
Dans l'espace vectoriel
![]() des polynômes, considérons les
deux familles suivantes :
des polynômes, considérons les
deux familles suivantes :
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales