Polynômes de Lagrange

Même s'ils le font très vite, il n'y a guère qu'une chose que les ordinateurs sachent faire avec des nombres : les ajouter et les multiplier, donc évaluer des fonctions polynômes. Si on doit effectuer des calculs sur une fonction quelconque, il est important de pouvoir l'approcher par des fonctions polynômes. Selon le sens précis que l'on donne à «approcher», il existe une grande variété de techniques, et autant de familles de polynômes qui leur sont adaptées. Nous traitons ici une des questions les plus simples : comment construire un polynôme de degré minimal, dont le graphe passe par certains points du plan. C'est le problème de l'interpolation. Nous commençons par nous donner les abscisses des points. Ce sont réels, $a_1,\ldots,a_n$ , différents deux à deux. Nous définissons maintenant polynômes $L_1,\ldots,L_n$ , de degré $n\!-\!1$ , qui sont tels que et pour $j\neq i$ .

Définition 12 On appelle polynômes interpolateurs de Lagrange aux abscisses
$a_1,\ldots,a_n$ , les polynômes $L_1,\ldots,L_n$ , définis pour $i=1,\ldots,n$ par :

$\displaystyle L_i(X) = \prod_{j\neq i} \frac{X-a_j}{a_i-a_j}\;.$

Voici les trois polynômes associés aux abscisses

$\displaystyle L_1(X) = \frac{X-4}{2-4} \frac{X-5}{2-5}\;,\quad L_2(X) = \frac{... ...-2} \frac{X-5}{4-5}\;,\quad L_3(X) = \frac{X-2}{5-2} \frac{X-4}{5-4}\;,\quad$

Nous sommes intéressés par les combinaisons linéaires des

. Prenons

réels $b_1,\ldots,b_n$ , et formons le polynôme

$\displaystyle P(X) = b_1 L_1(X)+\cdots+b_n L_n(X)\;.$

Remplaçons

par

. Tous les termes

s'annulent, sauf

qui vaut

. Donc

. La fonction polynôme $x\mapsto P(x)$ passe par les

points $(a_1,b_1),\ldots, (a_n,b_n)$ : elle les interpole. Par exemple pour

$\displaystyle P(X) = 3 L_1(X)+2 L_2(X)+3 L_3(X) = \frac{5}{6} X^2-\frac{11}{2} X+\frac{32}{3}\;.$

La figure 3 représente le graphe de

**Figure 3:** Interpolation par un polynôme de Lagrange des points d'abscisses et d'ordonnées .
$\includegraphics[width=10cm]{lagrange}$

Le polynôme

ainsi construit est le seul polynôme de degré $\leqslant n-1$ qui interpole les points $(a_1,b_n),\ldots,(a_n,b_n)$ : on le déduit de la proposition suivante.

Proposition 13 Les polynômes $L_1(X),\ldots,L_n(X)$ forment une base de l'espace vectoriel des polynômes de degré $\leqslant n-1$ .

Démonstration : Comme la dimension de l'espace est

, il suffit de montrer que la famille $\big( L_1(X),\ldots,L_n(X) \big)$ est libre. Considérons une combinaison linéaire, et supposons qu'elle est nulle.

$\displaystyle P(X) = b_1 L_1(X)+\cdots+b_n L_n(X) = 0\;.$

Comme pour tout $i=1,\ldots,n$ ,

, on doit avoir

. D'où le résultat. $\square$

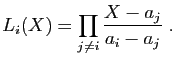
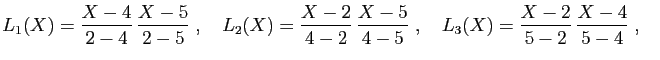
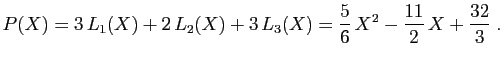
Les valeurs $b_1,\ldots,b_n$ sont les coordonnées du polynôme dans la base
$\big( L_1(X),\ldots,L_n(X) \big)$ .