Les équations différentielles linéaires sont très proches des
équations de récurrence traitées ci-dessus.
Considérons
l'équation 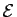 :
:
où
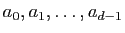 sont
sont 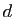 coefficients réels,
coefficients réels, 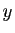 est
une fonction indéfiniment dérivable, et
est
une fonction indéfiniment dérivable, et
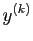 désigne sa dérivée
désigne sa dérivée 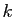 -ième.
Pour connaître la
forme des solutions de
-ième.
Pour connaître la
forme des solutions de
 , il faut résoudre
l'équation suivante :
, il faut résoudre
l'équation suivante :
Cette équation porte aussi le nom d'équation caractéristique
associée. C'est
la condition pour que
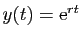 soit solution de
soit solution de
 .
.
Le résultat suivant est l'analogue du théorème 9 et
sa démonstration est très proche.
En pratique, pour déterminer
une solution vérifiant 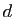 conditions particulières, il suffit de
calculer ses coefficients
conditions particulières, il suffit de
calculer ses coefficients
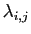 en résolvant un système
linéaire ordinaire, de
en résolvant un système
linéaire ordinaire, de 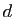 équations à
équations à 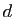 inconnues.
Exemple : Considérons l'équation suivante :
inconnues.
Exemple : Considérons l'équation suivante :
L'équation caractéristique associée est :
Cette équation a pour racines 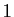 (racine simple) et
(racine simple) et 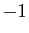 (racine double).
Toute solution de l'équation différentielle s'écrit donc :
(racine double).
Toute solution de l'équation différentielle s'écrit donc :
Pour trouver la solution qui vérifie 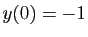 ,
, 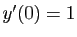 ,
,
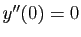 , on résout le système suivant.
, on résout le système suivant.
La solution est 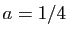 ,
, 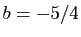 ,
, 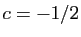 . La fonction cherchée
est donc :
. La fonction cherchée
est donc :
Il se peut que l'équation caractéristique associée admette des
racines complexes conjuguées.
Supposons que
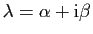 soit
racine de
soit
racine de 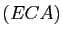 , alors
, alors
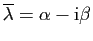 est aussi solution. Donc
est aussi solution. Donc
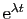 ,
,
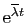 et toutes leurs combinaisons linéaires sont
solutions de
et toutes leurs combinaisons linéaires sont
solutions de
 . En particulier :
. En particulier :
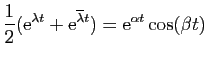
et
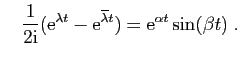
Parmi les solutions réelles de
 , on trouvera donc
toutes les combinaisons linéaires de ces deux fonctions.
, on trouvera donc
toutes les combinaisons linéaires de ces deux fonctions.
L'ensemble des solutions réelles de
 est un espace
vectoriel de dimension
est un espace
vectoriel de dimension 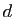 sur
sur
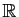 .
Exemple : Considérons l'équation suivante.
.
Exemple : Considérons l'équation suivante.
L'équation caractéristique associée est :
Ses racines sont :
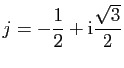
et
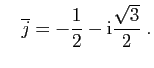
Toute solution réelle de l'équation différentielle s'écrit :
Cette équation pourrait correspondre aux petites oscillations d'un pendule
en milieu visqueux. Les solutions trouvées tendent vers 0, avec des
oscillations de plus en plus atténuées.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() :
:
![]() les racines (réelles ou complexes) de
l'équation
caractéristique associée
les racines (réelles ou complexes) de
l'équation
caractéristique associée ![]() et
et
![]() leurs
multiplicités. Toute solution de l'équation
leurs
multiplicités. Toute solution de l'équation
![]() s'écrit :
s'écrit :
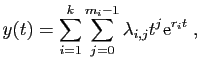
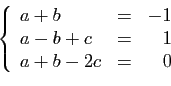
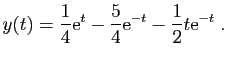
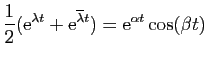 et
et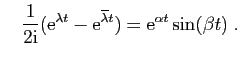
![]() est un espace
vectoriel de dimension
est un espace
vectoriel de dimension ![]() sur
sur
![]() .
Exemple : Considérons l'équation suivante.
.
Exemple : Considérons l'équation suivante.
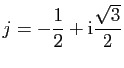 et
et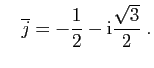
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales