Une application entre deux ensembles est injective si deux
éléments distincts de ![]() n'ont jamais la même image par
n'ont jamais la même image par ![]() .
Le vecteur nul de
.
Le vecteur nul de ![]() a
pour image par
a
pour image par ![]() , le vecteur nul de
, le vecteur nul de ![]() . Puisque
. Puisque ![]() est injective,
aucun vecteur non nul de
est injective,
aucun vecteur non nul de ![]() ne peut avoir pour image 0. Donc
Ker
ne peut avoir pour image 0. Donc
Ker![]() .
.
Montrons maintenant la réciproque. Supposons
Ker![]() . Soient
. Soient ![]() et
et ![]() deux éléments de
deux éléments de ![]() tels
que
tels
que ![]() . Puisque
. Puisque ![]() est linéaire,
est linéaire,
![]() . Donc
. Donc
![]() Ker
Ker![]() , donc
, donc ![]() , donc
, donc ![]() .
.
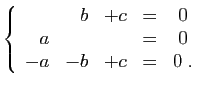
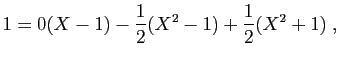
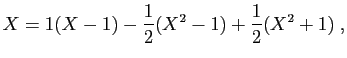
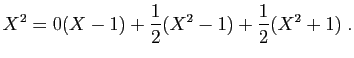
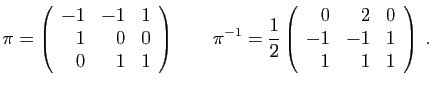
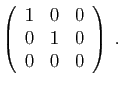
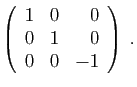
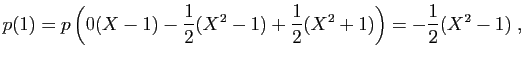
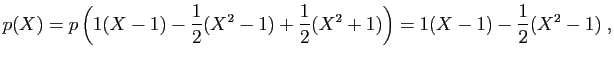
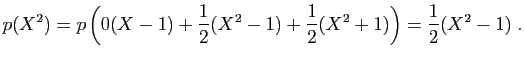
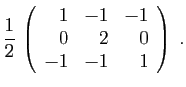
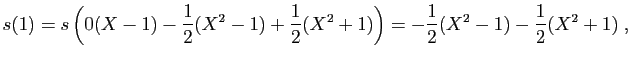
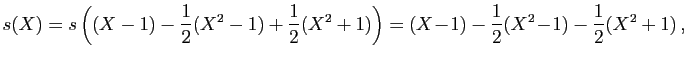
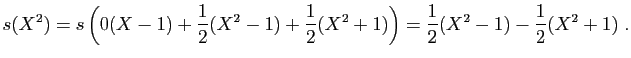
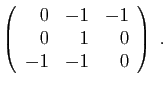
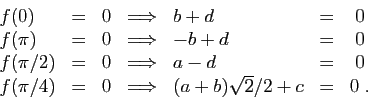
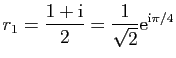 et
et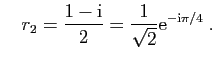
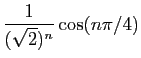 et
et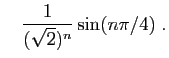
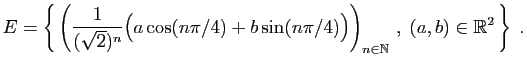
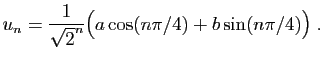
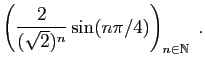
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales