-
 Ensemble des suites bornées.
Ensemble des suites bornées.
 Ensemble des suites décroissantes
à partir d'un certain rang.
Ensemble des suites décroissantes
à partir d'un certain rang.
-
 Ensemble des suites périodiques.
Ensemble des suites périodiques.
-
 Ensemble des suites convergeant vers 0.
Ensemble des suites convergeant vers 0.
 Ensemble des suites monotones.
Ensemble des suites monotones.
 Ensemble des suites équivalentes à
Ensemble des suites équivalentes à 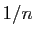 .
.
-
 Ensemble des suites dominées par
Ensemble des suites dominées par 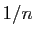 .
.
-
 Ensemble des suites négligeables devant
Ensemble des suites négligeables devant 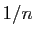 .
.
 Ensemble des suites dont le terme général est
Ensemble des suites dont le terme général est
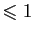 à partir
d'un certain rang.
à partir
d'un certain rang.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales