D'après certains auteurs, l'histoire des équations
différentielles commence en 1675,
le jour où Gottfried Wilhelm von Leibniz (1646-1716), co-inventeur du
calcul différentiel avec Newton, écrit :
Ne vous moquez pas, c'était un pas de géant. Jusque-là personne
n'avait vu le rapport entre le calcul des tangentes
à une courbe, et le calcul des
surfaces délimitées par une autre courbe.
Très vite Newton proposa de ranger les nombreux
problèmes issus de la mécanique en trois classes :
-
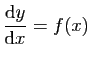
-
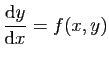
-
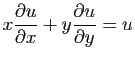
La première classe concerne le calcul direct de primitives. De la
seconde relèvent les équations diférentielles «ordinaires»
étudiées dans ce chapitre. La troisième classe fait partie de
ce que l'on appelle aujourd'hui les équations aux dérivées
partielles. Les nouveaux outils se révélèrent
extrêmement puissants pour aborder tous ces problèmes. Leur
résolution allait occuper pratiquement tout le XVIIIe siècle,
avec d'abord les contributions de Leibniz lui-même, puis ses émules
Suisses, les frères Bernoulli, et plus tard Euler
(1707-1783), puis en France Lagrange (1736-1813) et d'Alembert
(1717-1783). On peut dire qu'en 1775, un siècle après la
découverte du calcul différentiel, l'essentiel des méthodes de
résolution explicite d'équations différentielles avait été
trouvé.
Nous allons traiter deux problèmes de
mécanique, qui suscitèrent une réelle compétition chez les
mathématiciens du début du XVIIIe siècle.
La chaînette est la courbe
que décrit une chaîne ou une corde très souple
lorsqu'on la suspend par ses
deux extrémités (figure 6).
Considérons que la position de la corde est
rapportée à un repère dans le plan vertical, et examinons la
portion de corde comprise entre les abscisses 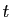 et
et
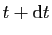 .
Lorsque la corde est immobile, trois forces
s'équilibrent pour cette portion : la traction de la
partie gauche de la corde, le poids du tronçon entre
.
Lorsque la corde est immobile, trois forces
s'équilibrent pour cette portion : la traction de la
partie gauche de la corde, le poids du tronçon entre 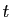 et
et
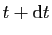 , et la traction de la partie droite. Donc la différence entre
les composantes verticales des tractions à
gauche et à droite doit équilibrer le poids du
tronçon. Désignons par
, et la traction de la partie droite. Donc la différence entre
les composantes verticales des tractions à
gauche et à droite doit équilibrer le poids du
tronçon. Désignons par 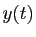 la hauteur du tronçon d'abscisse
la hauteur du tronçon d'abscisse
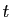 . Les tractions gauche et droite s'exercent
tangentiellement en chaque point de la courbe ; leur composante
verticale est proportionnelle à la dérivée de
. Les tractions gauche et droite s'exercent
tangentiellement en chaque point de la courbe ; leur composante
verticale est proportionnelle à la dérivée de 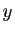 . La
différence entre la traction à droite et à gauche s'écrit :
. La
différence entre la traction à droite et à gauche s'écrit :
Si la corde est supposée homogène, le
poids du tronçon entre 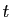 et
et
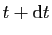 est proportionnel à sa
longueur, qui d'après le théorème de Pythagore vaut :
est proportionnel à sa
longueur, qui d'après le théorème de Pythagore vaut :
La dérivée de 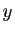 est donc solution de l'équation du
premier ordre :
est donc solution de l'équation du
premier ordre :
où 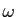 est un coefficient de proportionnalité. L'ensemble des
solutions de cette équation est :
est un coefficient de proportionnalité. L'ensemble des
solutions de cette équation est :
Rappelons que le sinus et le cosinus hyperboliques sont définis
par :
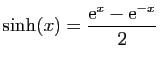
et
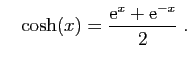
Si comme sur la figure 6 on a choisi le repère de
sorte que pour 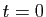 la tangente soit
horizontale et l'ordonnée nulle (
la tangente soit
horizontale et l'ordonnée nulle (
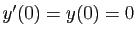 ), alors :
), alors :
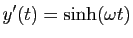
et

Voici maintenant le problème de la tractrice.
Un enfant marche au bord d'un bassin rectiligne, en tirant un
bateau au bout d'une corde. Au départ, la corde est perpendiculaire
au bord du bassin. L'enfant se déplace à vitesse constante, et la
vitesse du bateau est toujours dirigée dans le sens de la corde, qui
reste toujours tendue. Quelle est la trajectoire du bateau dans le
bassin ?
Choisissons un repère orthonormé du plan, dans lequel le bord du
bassin est sur l'axe horizontal, et l'origine au point où l'enfant
commence à marcher (figure 7).
À l'instant 0, le bateau se trouve donc au
point d'abscisse 0 et d'ordonnée  , la longueur de la corde.
Notons
, la longueur de la corde.
Notons
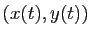 la position du bateau à l'instant
la position du bateau à l'instant 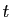 . Soit
. Soit 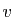 la vitesse à laquelle marche l'enfant. À l'instant
la vitesse à laquelle marche l'enfant. À l'instant 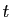 , l'enfant se
trouve au point
, l'enfant se
trouve au point 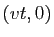 et la corde est tendue. Donc :
et la corde est tendue. Donc :
soit en dérivant :
D'autre part le vecteur vitesse du bateau,
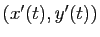 est colinéaire au
vecteur allant du bateau à l'enfant, donc :
est colinéaire au
vecteur allant du bateau à l'enfant, donc :
On obtient un système de deux équations différentielles :
Multiplions la première équation par 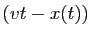 , la seconde par
, la seconde par
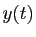 et ajoutons : les termes en
et ajoutons : les termes en 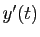 disparaissent et on
obtient :
disparaissent et on
obtient :
Or
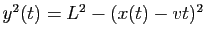 :
:
Après simplification on obtient :
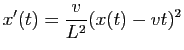 |
(9) |
Cette équation, où 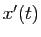 s'exprime par une expression
quadratique en
s'exprime par une expression
quadratique en 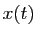 , est une équation de Riccati.
Jacopo Riccati (1676-1754), un comte italien de la région de Venise,
a montré que ce type d'équations apparaissait naturellement
dans différents problèmes, mais il
s'est bien gardé de les résoudre, laissant cela à Johann
Bernoulli et Leonhard Euler.
Puisque nous en sommes à comparer des exploits, signalons que
la comtesse Elisabetta dei Conti d'Onigo, épouse Riccati,
a porté 18 enfants, dont 9 ont vécu et 2 ont même
laissé un nom dans l'histoire, l'un de la physique, l'autre de la
musique. Madame Euler née Katharina Gsell en revanche n'a eu «que» 12
enfants dont 5 ont vécu. Il est vrai que
Riccati a moins de réalisations mathématiques
à son actif que son successeur Euler.
, est une équation de Riccati.
Jacopo Riccati (1676-1754), un comte italien de la région de Venise,
a montré que ce type d'équations apparaissait naturellement
dans différents problèmes, mais il
s'est bien gardé de les résoudre, laissant cela à Johann
Bernoulli et Leonhard Euler.
Puisque nous en sommes à comparer des exploits, signalons que
la comtesse Elisabetta dei Conti d'Onigo, épouse Riccati,
a porté 18 enfants, dont 9 ont vécu et 2 ont même
laissé un nom dans l'histoire, l'un de la physique, l'autre de la
musique. Madame Euler née Katharina Gsell en revanche n'a eu «que» 12
enfants dont 5 ont vécu. Il est vrai que
Riccati a moins de réalisations mathématiques
à son actif que son successeur Euler.
Revenons à l'équation de la tractrice (9). Elle a
une solution naturelle,
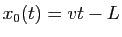 . C'est ce qui se passerait si le
bateau partait au bord du bassin, tiré horizontalement par l'enfant.
Posons :
. C'est ce qui se passerait si le
bateau partait au bord du bassin, tiré horizontalement par l'enfant.
Posons :
Cette nouvelle fonction est solution de l'équation linéaire
suivante.
La solution générale est
 . Si le
bateau démarre au point
. Si le
bateau démarre au point 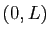 , alors
, alors 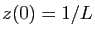 . On obtient :
. On obtient :
On en déduit alors :
De nombreuses courbes issues de la mécanique
furent ainsi étudiées tout au long du
XVIIIe siècle, et elles portent depuis des noms qui rappellent
leur origine.
- - vélaire :
- courbe d'une voile gonflée par le vent.
- - elastica :
- courbe que forme une poutre élastique
fixée à une seule de ses extrémités.
- - isochrone :
- courbe le long de laquelle un corps tombe avec
une vitesse uniforme.
- - brachistochrone :
- courbe le long de laquelle un corps tombe
d'un point à un autre en temps minimum.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
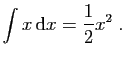
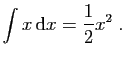
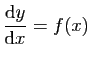
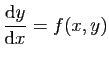
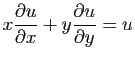
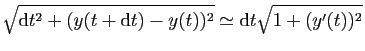
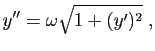
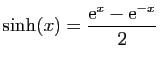 et
et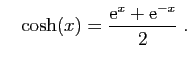

![]() , la longueur de la corde.
Notons
, la longueur de la corde.
Notons
![]() la position du bateau à l'instant
la position du bateau à l'instant ![]() . Soit
. Soit ![]() la vitesse à laquelle marche l'enfant. À l'instant
la vitesse à laquelle marche l'enfant. À l'instant ![]() , l'enfant se
trouve au point
, l'enfant se
trouve au point ![]() et la corde est tendue. Donc :
et la corde est tendue. Donc :
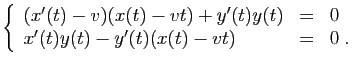
![]() . C'est ce qui se passerait si le
bateau partait au bord du bassin, tiré horizontalement par l'enfant.
Posons :
. C'est ce qui se passerait si le
bateau partait au bord du bassin, tiré horizontalement par l'enfant.
Posons :
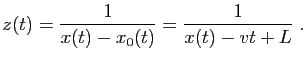
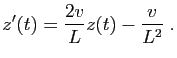
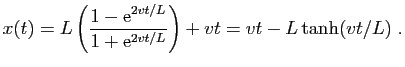
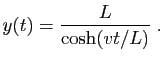
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales