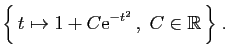
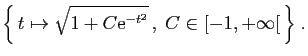
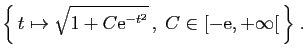
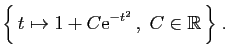
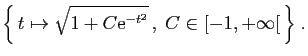
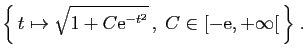
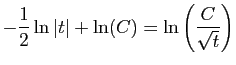 |
|||
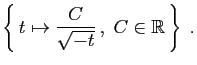
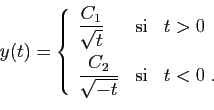
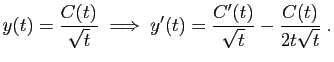
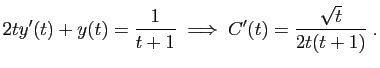
![$\displaystyle C(t)=\int_c^t \frac{\sqrt{s}}{2s(s+1)} \mathrm{d}s
=\int_{\sqrt{...
...mathrm{d}u
=\Big[\arctan(u)\Big]_{\sqrt{c}}^{\sqrt{t}}
=\arctan(\sqrt{t})+C\;.
$](img606.gif)
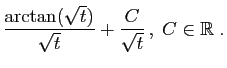
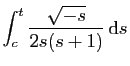 |
|||
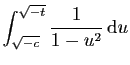 |
|||
![$\displaystyle \displaystyle{
\left[\frac{1}{2}
\ln\left\vert\frac{1+u}{1-u}\right\vert\right]_{\sqrt{c}}^{\sqrt{t}}}$](img615.gif) |
|||
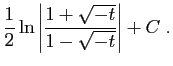 |
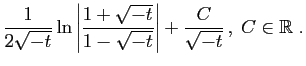
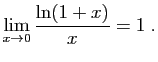
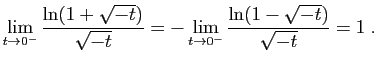
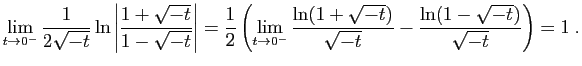
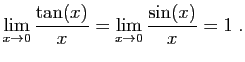
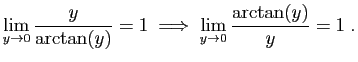
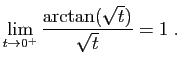
Toute solution de ![]() sur
sur
![]() doit aussi être solution
de
doit aussi être solution
de ![]() sur
sur ![]() et sur
et sur
![]() .
Or parmi les solutions de
.
Or parmi les solutions de ![]() sur
sur ![]() ,
, ![]() est la seule à
avoir une limite à gauche finie en 0.
De même sur
est la seule à
avoir une limite à gauche finie en 0.
De même sur
![]() ,
, ![]() est la seule à avoir une limite à droite finie en 0. Donc
est la seule à avoir une limite à droite finie en 0. Donc ![]() est la seule solution de
est la seule solution de ![]() sur
sur
![]() .
.
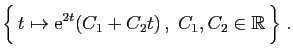
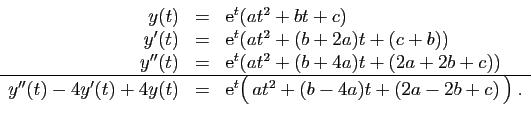
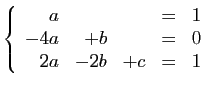
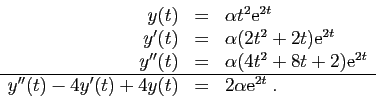
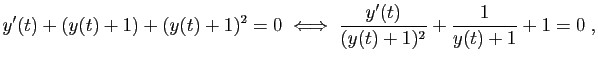
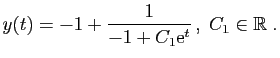
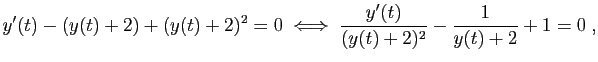
La solution générale de l'équation
![]() , est
, est
![]() . Donc la solution générale de
. Donc la solution générale de ![]() est :
est :
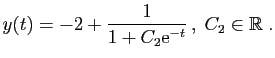
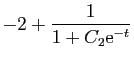 |
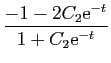 |
||
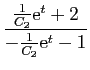 |
|||
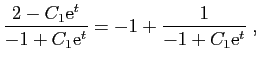 |
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales