-
-
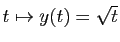 est solution de
est solution de 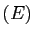 sur
sur
![$ ]0,+\infty[ $](img303.gif) .
.
-
-
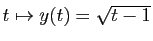 est la seule solution de
est la seule solution de
 sur
sur
![$ ]1,+\infty[ $](img485.gif) .
.
-
-
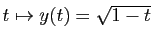 est solution de
est solution de
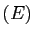 sur
sur
![$ ]-\infty,1[ $](img488.gif) .
.
-
- Pour tout
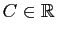 ,
,
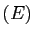 possède des solutions définies sur
possède des solutions définies sur
![$ ]C,+\infty[ $](img490.gif) .
.
-
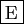
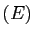 possède des solutions définies sur
possède des solutions définies sur
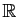 .
.
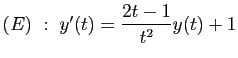 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales