Programmation

Le langage Xcas permet d'écrire des programmes, comme n'importe quel langage de programmation. Voici ses principales caractéristiques.

$\bullet$

C'est un langage fonctionnel. L'argument d'une fonction peut être une autre fonction. Si c'est le cas, on peut soit donner le nom de la fonction argument dans la commande, soit sa définition : par exemple function_diff(f) ou bien function_diff(x->x^2).

$\bullet$

Il n'y a pas de distinction entre programme et fonction : une fonction renvoie la valeur de la dernière instruction évaluée ou ce qui suit le mot réservé return. Comme pour tous les environnements de calcul, programmer consiste à étendre Xcas en lui rajoutant les fonctions souhaitées. Structurer la programmation consiste à hiérarchiser les différentes fonctions qui s'appellent entre elles.

$\bullet$

Le langage est non typé. On distingue seulement les variables globales, qui ne sont pas déclarées, et les variables locales, déclarées en début de fonction.

Dans un programme, lorsqu'on appelle une variable munie d'un indice, c'est une table qui est créée, et non une liste. Une table est un conteneur d'objets analogue aux listes et aux séquences. La différence est qu'elle peut être indicée par autre chose qu'un entier, par exemple une chaîne de caractères. Si a est une variable formelle, la commande a[1]:=2 crée une table a. Pour que a soit une liste, il faut d'abord affecter a avec une liste, et la modifier ensuite. Par exemple a:=[0$10] (si on connaît a priori la taille de la liste) ou a:=[]; (affecter la liste vide). Même si le langage est non typé, il est donc recommandé d'initialiser les variables avant de les utiliser. La syntaxe de déclaration d'une fonction est la suivante.

nom_fonction(var1,var2,...):=
{
local var_loc1, var_loc2,... ;
  instruction1;
  instruction2;
  ...
}

La syntaxe des tests et des boucles est celle du langage C++. Pour les tests :

if (condition) {clause_vraie} else {clause_fausse}

(le else est facultatif). La condition est un booléen, résultat d'une expression logique, utilisant les opérateurs habituels.

Opérateurs logiques
==	$=$	!=	non
<	$<$	>	$>$
<=	$\leqslant$	>=	$\geqslant$
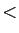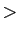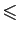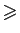&&	et	||	ou

Par exemple :

testif(a,b):={
if ( (a==10) || (a<b) )
    b:=b-a;
else 
    a:=a-b;
return [a,b];
};

La syntaxe de for est la suivante.

for(initialisation;test;incrementation){ corps_de_boucle }

Par exemple :

testfor(a,b):={
local j,(s:=0);
for (j:=a;j<=b;j++)
   s:=s+1/j^2;
   return s;
};

Attention, i désigne 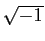$\sqrt{-1}$ et ne peut pas être utilisé comme variable de boucle. L'instruction break; permet de sortir d'une boucle et continue; de passer immédiatement à l'itération suivante. De nombreuses variantes sont reconnues en particulier en mode de compatibilité avec Maple, Mupad et les TI89/Voyage 200. On peut capturer des erreurs d'exécution par

try {bloc_erreurs_capturees} 
catch (variable)
    {bloc_execute_si_erreur}

Par exemple :

try{A:=idn(2)*idn(3)} 
catch(erreur) 
{print("l'erreur est "+erreur)}

Quelques exemples Pour écrire un programme, il est conseillé d'ouvrir un éditeur de programme avec le menu Add->Programme. Le menu Prog de l'éditeur permet d'entrer facilement les structures de programmation. On peut ensuite sauvegarder le texte du programme indépendamment de la session de travail pour l'utiliser ensuite dans une autre session de travail.

Voici un programme qui donne le quotient et le reste de la division euclidienne de 2 entiers en utilisant les fonctions iquo qui renvoie le quotient et irem qui renvoie le reste (c'est la fonction iquorem de Xcas).

  idiv2(a,b):={ 
    local q,r;
    if (b!=0) {
      q:=iquo(a,b);
      r:=irem(a,b);
    }
    else {
      q:=0;
      r:=a;
    }
    return [q,r];
  }

Saisissez cette fonction dans un éditeur de programme, testez-la (bouton OK) puis sauvegardez par exemple sous le nom idiv2.cxx. Vous pouvez utiliser cette fonction dans une ligne de commande, en tapant par exemple idiv2(25,15). Vous pourrez utiliser cette fonction dans une autre session Xcas, en utilisant la commande read("idiv2.cxx") ou en l'ouvrant depuis un éditeur de programme (et en le validant par OK).

Voici maintenant deux versions du calcul du PGCD de deux entiers, une version itérative, puis une version récursive.

pgcd_iteratif(a,b):={
 local r;
 while (b!=0) {
    r:=irem(a,b);
    a:=b;
    b:=r;
 }
 return a;
};

pgcd_recursif(a,b):={
 if (b==0) return a;
 return pgcd_recursif(b,irem(a,b));
};

Il arrive parfois qu'un programme ne fonctionne pas du premier coup comme prévu (!) Il est possible de l'exécuter en mode pas-à-pas pour le mettre au point, avec la commande debug. Pour plus de détails consulter le menu Aide->Interface. Par exemple, pour le programme idiv2, on lance la mise au point en tapant debug(idiv2(25,15)). On peut visualiser l'état des variables a,b,r avec le bouton watch et exécuter instruction par instruction avec le bouton sst. Style de programmation Xcas est interprété et non compilé. Plus que le nombre de lignes du programme, c'est le nombre d'instructions réellement exécutées qui influence le temps de calcul. En règle générale, il est plus rapide de créer des listes ou des séquences que de programmer des boucles. Voici quelques manières de calculer 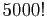$5000!$ : comparez leurs temps d'exécution.

5000!
product([n$(n=1..5000)])
product(cumSum([1$5000]))
f:=1; (f:=f*n)$(n=2..5000):;f
f:=1; for(n:=1;n<=5000;n++) {f:=f*n}
f:=1;n:=1; while(n<5000) {n:=n+1; f:=f*n}

La rapidité d'exécution est parfois contradictoire avec la clarté du programme, et on doit accepter des compromis. Dans une utilisation courante, le temps de calcul n'est pas réellement un enjeu : on utilise en général les langages interprétés comme Xcas pour tester des algorithmes et réaliser des maquettes. Les applications en vraie grandeur sont codées dans des langages compilés comme C++.