Arithmétique des entiers
Les opérations sur les entiers figurent dans le menu
Math->Integer.
Les calculs modulo 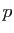 se font en
utilisant
se font en
utilisant %p. Une fois défini un entier modulo 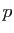 , disons
, disons
a:=3%5, tous les calculs seront effectués dans
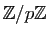 :
: a*2 renvoie 1%5 (6 modulo 5),
1/a renvoie 2%5, ...
Pour calculer efficacement les puissances modulo 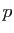 , on peut utiliser ce qui
précède, ou la fonction
, on peut utiliser ce qui
précède, ou la fonction powermod.
a:=3%5
a+12
a^4
powermod(3,4,5)
| Nombres entiers |
a%p |
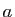 modulo modulo 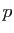 |
powermod(a,n,p) |
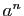 modulo modulo 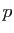 |
irem |
reste de la division euclidienne |
iquo |
quotient de la division euclidienne |
iquorem |
quotient et reste |
ifactor |
décomposition en facteurs premiers |
ifactors |
liste des facteurs premiers |
idivis |
liste des diviseurs |
gcd |
plus grand diviseur commun |
lcm |
plus petit multiple commun |
iegcd |
identité de Bézout |
iabcuv |
renvoie ![$ [u,v]$](img50.gif) tels que tels que 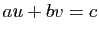 |
is_prime |
l'entier est-il premier |
nextprime |
prochain entier premier |
previousprime |
entier premier précédent |
Polynômes et fractions rationnelles
Les fonctions de traitement des polynômes figurent dans le menu
Alg->Polynomes.
On utilise normal ou expand
pour développer, ou plus généralement mettre une fraction
sous forme irréductible, et factor pour
factoriser. Le résultat dépend du corps de nombres dans lequel on
se place. Par défaut il s'agit des réels. Pour les complexes, il
faut activer l'option Complex à partir du bouton rouge
cas. On peut aussi déclarer les coefficients comme des
entiers modulo 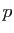 pour travailler dans
pour travailler dans
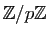 . Exécutez les
commandes suivantes avant et après avoir activé l'option
. Exécutez les
commandes suivantes avant et après avoir activé l'option
Complex.
P:=x^4-1
factor(P)
divis(P)
propfrac(x^4/P)
partfrac(4/P)
Q:=(x^4+1)%3
factor(Q)
genpoly(5,3,x)
genpoly(2,3,x)
genpoly(2*y+5,3,x)
| Polynômes |
normal |
forme normale (développée et réduite) |
expand |
forme développée |
ptayl |
forme de Taylor |
peval ou horner |
évaluation en un point par l'algorithme de Horner |
genpoly |
polynôme défini par sa valeur en un point |
canonical_form |
trinôme sous forme canonique |
coeff |
liste des coefficients |
poly2symb |
de l'expression algébrique à la forme symbolique |
symb2poly |
de la forme symbolique à l'expression algébrique |
pcoeff |
polynôme décrit par ses racines |
degree |
degré |
lcoeff |
coefficient du terme de plus haut degré |
valuation |
degré du monôme de plus bas degré |
tcoeff |
coefficient du terme de plus bas degré |
factor |
décomposition en facteurs premiers |
factors |
liste des facteurs premiers |
divis |
liste des diviseurs |
collect |
factorisation sur les entiers |
froot |
racines avec leurs multiplicités |
proot |
valeurs approchées des racines |
sturmab |
nombre de racines dans un intervalle |
getNum |
numérateur d'une fraction rationnelle |
getDenom |
dénominateur d'une fraction rationnelle |
propfrac |
isole partie entière et fraction propre |
partfrac |
décomposition en éléments simples |
quo |
quotient de la division euclidienne |
rem |
reste de la division euclidienne |
gcd |
plus grand diviseur commun |
lcm |
plus petit multiple commun |
egcd |
identité de Bézout |
divpc |
division suivant les puissances croissantes |
randpoly |
polynôme aléatoire |
cyclotomic |
polynômes cyclotomiques |
lagrange |
polynômes de Lagrange |
hermite |
polynômes de Hermite |
laguerre |
polynômes de Laguerre |
tchebyshev1 |
polynômes de Tchebyshev |
tchebyshev2 |
polynômes de Tchebyshev |
Trigonométrie
Le menu Math->Transcendental contient
les fonctions circulaires et hyperboliques ainsi que leurs inverses.
Pour linéariser et
développer on utilise tlin et texpand. Beaucoup
d'autres récritures sont accessibles à partir des menus
Math->Recriture_trig : transformation des tangentes en sinus et
cosinus
(tan2sincos), transformations en
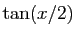 (
(halftan),...
Math->Recriture_trig_exp : transformation des fonctions
trigonométriques en exponentielles par les
formules d'Euler (trig2exp), des exponentielles en
fonctions trigonométriques (exp2trig),
des exponentielles en puissances (exp2pow)...,
Math->Recriture_trig_inv : transformation des fonctions inverses
exp2pow(exp(3*ln(x)))
exp2trig(exp(i*x))
trig2exp(cos(x))
E:=sin(x)^4+sin(x)^3
El:=tlin(E)
texpand(El)
tsimplify(E)
tsimplify(El)
tsimplify(E-El)
halftan(E)
trig2exp(El)
Et:=trigtan(E)
tan2sincos(Et)
tan2sincos2(Et)
tan2cossin2(Et)
| Trigonométrie |
tlin |
linéariser |
tcollect |
linéariser et regrouper |
texpand |
forme polynomiale |
trig2exp |
trigonométrique vers exponentielle |
exp2trig |
exponentielle vers trigonométrique |
hyp2exp |
hyperbolique vers exponentielle |
Vecteurs et matrices
Un vecteur est une liste de nombres, une matrice est la liste de ses
vecteurs lignes. Le produit matriciel est noté comme le produit
ordinaire par une étoile. Les vecteurs sont a priori des vecteurs lignes,
mais le produit à droite par un vecteur ligne est effectué comme
si c'était une colonne. En particulier, si v et w
sont deux vecteurs de même taille, v*w retourne leur produit
scalaire.
A:=[[1,2,3],[4,5,6],[7,8,9]]
v:=[1,1,1]
v*v
A*v
v*A
B:=[[1,1,1],[2,2,2]]
A*B
B*A
A*tran(B)
À partir d'une fonction qui à deux indices 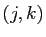 associe un réel
associe un réel
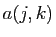 , on peut constituer une matrice avec
, on peut constituer une matrice avec makemat ou
matrix. Pour makemat les indices commencent à 0, pour
matrix il commencent à 1.
makemat((j,k)->j+2*k,3,2)
matrix(3,2,(j,k)->j+2*k)
On peut aussi créer des matrices par blocs avec la commande
blockmatrix.
A:=makemat((j,k)->j+2*k,3,2)
B:=idn(3)
blockmatrix(1,2,[A,B])
blockmatrix(2,2,[A,B,B,A])
On accède à un élément d'une matrice grâce à deux indices
séparés par une virgule et mis entre
crochets. Le premier indice est l'indice de la ligne et le deuxième
celui de la colonne. Les indices commencent à 0.
Par exemple, si A:=[[0,2],[1,3],[2,4]] alors
A[2,1] renvoie 4.
Pour extraire un bloc de la matrice, on utilise des intervalles
comme indices : A[1..2,0..1] renvoie le bloc
constitué des lignes 1 à 2 et des colonnes 0 à 1.
Notez que les matrices de Xcas sont
recopiées entièrement à chaque modification d'un coefficient.
Ceci est pénalisant si on modifie successivement
dans un programme beaucoup
de coefficients d'une même (grande) matrice.
| Vecteurs et matrices |
v*w |
produit scalaire |
cross(v,w) |
produit vectoriel |
A*B |
produit matriciel |
A.*B |
produit terme à terme |
1/A |
inverse |
tran |
transposée |
rank |
rang |
det |
déterminant |
ker |
base du noyau |
image |
base de l'image |
idn |
matrice identité |
ranm |
matrice à coefficients aléatoires |
Systèmes linéaires
Il existe trois moyens différents de résoudre un système
linéaire.
- La fonction
linsolve résout une liste d'équations
linéaires, avec la même syntaxe que solve.
- La fonction
simult peut résoudre plusieurs systèmes d'équations linéaires
qui ne diffèrent que par leur second membre. Elle prend comme premier
argument la matrice du système et comme second argument la matrice dont la
(ou les) colonnes sont le (ou les) second membre(s) des systèmes.
- La fonction
rref calcule la réduction d'une matrice
quelconque sous forme de Gauss-Jordan. Si on borde
la matrice du système avec le second membre, rref retourne
une matrice contenant le vecteur solution.
Quand le système est impossible, linsolve retourne
la liste vide, simult retourne un message d'erreur, rref
retourne une matrice dont une des lignes est nulle, sauf le dernier
coefficient. Quand le système est indéterminé, linsolve
retourne la solution fonction de certaines variables, simult
retourne seulement une solution, rref retourne une matrice dont
une ou plusieurs lignes sont nulles. L'exemple ci-dessous concerne
le système :
Il a une solution unique pour 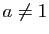 et
et 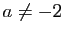 , il est impossible pour
, il est impossible pour
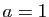 et il est indéterminé pour
et il est indéterminé pour 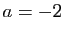 .
.
linsolve([x+y+a*z=1,x+a*y+z=1,x+a*y+z=-2],[x,y,z])
a:=1
linsolve([x+y+a*z=1,x+a*y+z=1,x+a*y+z=-2],[x,y,z])
a:=-2
linsolve([x+y+a*z=1,x+a*y+z=1,x+a*y+z=-2],[x,y,z])
purge(a)
A:=[[1,1,a],[1,a,1],[a,1,1]]
solve(det(A),a)
A1:=subst(A,a=1)
rank(A1)
image(A1)
ker(A1)
A2:=subst(A,a=-2)
rank(A2)
image(A2)
ker(A2)
b:= [1,1,-2]
B:=tran(b)
simult(A,B)
simult(A1,B)
simult(A2,B)
M:=blockmatrix(1,2,[A,B])
rref(M)
rref(border(A,b))
rref(border(A1,b))
rref(border(A2,b))
| Systèmes linéaires |
linsolve |
résolution d'un système |
simult |
résolution simultanée de plusieurs systèmes |
rref |
réduction de Gauss-Jordan |
rank |
rang |
det |
déterminant du système |
Réduction des matrices
La fonction jordan prend en entrée une matrice 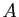 et retourne en
sortie une matrice de passage
et retourne en
sortie une matrice de passage 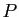 et une forme réduite de Jordan
et une forme réduite de Jordan 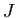 telles
que
telles
que
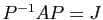 . Soit
. Soit 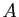 est diagonalisable auquel cas
est diagonalisable auquel cas 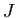 est
diagonale et contient les valeurs propres de
est
diagonale et contient les valeurs propres de 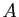 sur la diagonale,
soit
sur la diagonale,
soit 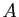 n'est pas diagonalisable et
n'est pas diagonalisable et 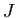 comporte des "1" ou des "0"
au-dessus de la diagonale. Pour les matrices exactes et symboliques,
seules les valeurs propres calculables par
comporte des "1" ou des "0"
au-dessus de la diagonale. Pour les matrices exactes et symboliques,
seules les valeurs propres calculables par
solve sont accessibles. Pour des matrices de nombres approchés,
un algorithme numérique est utilisé, et il risque
d'échouer en cas de valeurs propres multiples ou très proches.
La matrice 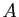 de l'exemple qui suit a pour valeurs propres doubles 1
et 2. Elle est diagonalisable pour
de l'exemple qui suit a pour valeurs propres doubles 1
et 2. Elle est diagonalisable pour
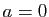 , non diagonalisable pour
, non diagonalisable pour 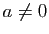 .
.
A:=[[1,1,-1,0],[0,1,0,a],[0,-1,2,0],[1,0,1,2]]
factor(poly2symb(simplify(pcar(A))))
jordan(A)
eigenvals(A)
eigenvects(A)
jordan(subs(A,a=0))
eigenvects(subs(A,a=1))
jordan(evalf(subs(A,a=0)))
jordan(evalf(subs(A,a=1)))
Certaines fonctions, définies par des séries
entières, s'étendent aux matrices dès lors que l'on sait calculer
leur forme de Jordan. La plus utile est l'exponentielle.
A:=[[0,1,0],[0,0,1],[-2,1,2]]
jordan(A)
exp(A)
log(A)
sin(A)
| Réduction des matrices |
jordan |
diagonalisation ou réduction de Jordan |
pcar |
coefficients du polynôme caractéristique |
pmin |
coefficients du polynôme minimal |
eigenvals |
valeurs propres |
eigenvects |
vecteurs propres |
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() se font en
utilisant
se font en
utilisant ![]() , disons
, disons
![]() :
: ![]() , on peut utiliser ce qui
précède, ou la fonction
, on peut utiliser ce qui
précède, ou la fonction ![]() pour travailler dans
pour travailler dans
![]() . Exécutez les
commandes suivantes avant et après avoir activé l'option
. Exécutez les
commandes suivantes avant et après avoir activé l'option
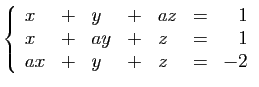
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales