v=[1:5]'. Quelles affirmations sont correctes,
lesquelles ne le sont pas et pourquoi ?

v*v'==v'*vdonne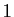

v*v'==v'*vdonneT-
v*v'est une matrice 
v*vest une matrice-
v'*v-norm(v).^2donne 0
v=[1:5]'. Quelles affirmations sont correctes,
lesquelles ne le sont pas et pourquoi ?
v*v'==v'*v donne v*v'==v'*v donne T
v*v' est une matrice
v*v est une matrice
v'*v-norm(v).^2 donne 0
A=[ 1:3 ; 2,2,2 ; 3:-1:1] et v=[3:-1:1]',
quelles affirmations sont correctes,
lesquelles ne le sont pas et pourquoi ?
v'*v vaut 14
v.*v vaut 14
v'*A*v est un réel
v==v(3:-1:1) donne v==v(3:-1:1) donne [ F T F ]'
v(3:-1:1)==A(:,1) donne [T T T]';
v(3:-1:1)==A(1,:) donne [T T T];
v=[1,2,3,4,5],
lesquelles ne l'affichent pas et pourquoi ?
v=[1;2;3;4;5]
v=[1,2,3,4,5];
[1:5]; v
v=[1:5]
v=[1:5];
[1:5]; v=ans
v=[1;5]
v=[1:10]; v(1,5)
v=[1:10]; v(1,[1:5])
v=linspace(1,5)
v=linspace(1,5,5)
v=cumsum(ones(1,5))
v=cumsum(ones(5,1))
v=find(ones(5,1)==1)
v=find(rand(1,5)<0)
v=find(rand(1,5)<1)
v=find(zeros(1,5)<=0)
v=sort([1,3,2,5,4])
v=sort([1;3;2;5;4]); v([5:-1:1])
v=sort([1,3,2,5,4]); v([5:-1:1])
v=gsort([1,3,2,5,4],"r","i")
v=gsort([1,3,2,5,4],"c","i")
v=gsort([1;3;2;5;4],"r","i"); v=v'
for i=1:5, v=i; end
for i=1:5, v=[v,i]; end; v
v=[]; for i=1:5, v=[v,i]; end; v
v=1; for i=1:5, v=[v,v($)+1]; end; v
v=1; for i=1:4, v=[v,v($)+1]; end; v
i=0; v=i; while i<=5, i=i+1; v=[v,i]; end; v
i=1; v=i; while i<=5, i=i+1; v=[v,i]; end; v
i=1; v=i; while i<5, i=i+1; v=[v,i]; end; v
v=[1,0.5,0.25,0.125,0.0625],
lesquelles ne l'affichent pas et pourquoi ?
2^(-[0:4])
1/2^[0:4]
(1)/2^[0:4]
(1)./2^[0:4]
v=cumprod(ones(1,5)/2)
v=[1,cumprod(ones(1,4)/2)]
v=cumprod([1,0.5*ones(1,4)])
for i=0:4, v=2^(-i); end;
v=[]; for i=0:4, v=[v,2^(-i)]; end; v
v=[1]; for i=1:4, v=[v,v/2]; end; v
x=1; v=[x]; for i=1:4, x=x/2; v=[v,x]; end; v
x=1; v=[x]; for i=1:4, v=[v,x/2]; end; v
x=1; v=[x]; while x>0.06, x=x/2; v=[v,x]; end; v
x=1; v=[x]; while x>0.1, x=x/2; v=[v,x]; end; v
A,
dont la première ligne est le vecteur
[0,1] et la deuxième ligne est le vecteur [1,0],
lesquelles ne l'affichent pas et pourquoi ?
A=[0,1;1,0]
A=[0,1]; A=[A,[1,0]]
A=[0,1]; A=[A;[1,0]]
A=[0;1]; A=[A;[1;0]]
A=[0;1]; A=[A,[1;0]]
A=[0,1]; A=A+A'
A=[0,1]; A=[A;A]
A=[0,1]; A=[A;A([2,1])]
A=[0,1]; A=[A;A(2,1)]
A(1,2)=1; A(2,1)=1
A=ones(2,2); A(1,1)=0; A(2,2)=0
A=eye(2,2)
A=ones(2,2)-eye(2,2)
A=ones(2,2)-diag(ones(1,2))
A=matrix([0,1,0,1],2,2)
A=matrix([0,1,1,0],2,2)
A=matrix([0;1;1;0],2,2)
A=[1,0]*[0;1]+[0,1]*[1;0]
A=[1;0]*[0,1]+[0;1]*[1,0]
U=ones(2,2); U(1,2)=-1; A=U*diag([1,-1])*U'
U=ones(2,2); U(1,2)=-1; A=U*diag([1,-1])*U'/2
A=toeplitz(0,1)
A=toeplitz([0,1])
A=bool2s(eye(2,2)==2);
A=bool2s([1,2;2,3]==2)
A,
dont les coefficients d'ordre A=eye(10,10)
A=[zeros(9,1),eye(9,9);zeros(1,10)]
for i=1:9, A(i,i+1)=1; end; A
A=zeros(10,10); for i=1:9, A(i,i+1)=1; end; A
for i=1:10, for j=1:10, if j==i+1 then A(i,j)=1;..
else A(i,j)=0; end; end; A
for i=1:10, for j=1:10, if j==i+1 then A(i,j)=1;..
else A(i,j)=0; end; end; end; A
A=toeplitz([0,1,zeros(1,8)])
A=toeplitz(zeros(10,1),[0,1,zeros(1,8)])
A,
dont les coefficients d'ordre A=eye(10,10)
A=[zeros(9,1),eye(9,9);zeros(1,10)]; A=A+A'
A=zeros(10,10); for i=1:9, A(i,i+1)=1; A(i+1,i)=1; end; A
for i=1:10, for j=1:10, if or(j==i+1,j==i-1) then A(i,j)=1;..
else A(i,j)=0; end; end; A
for i=1:10, for j=1:10, if or([j==i+1,j==i-1]) then A(i,j)=1;..
else A(i,j)=0; end; end; end; A
for i=1:10, for j=1:10, if j==i+1|j==i-1 then A(i,j)=1;..
else A(i,j)=0; end; end; end; A
A=toeplitz([1,zeros(1,9)])
A=toeplitz([0,1,zeros(1,8)])
v=zeros(1,2*n); v(2*[1:n])=[1:n]
v=zeros(1,2*n); v([1:n])=2*[1:n]
v=[zeros(1,n);[1:n]]; v=matrix(v,1,2*n)
v=[zeros(n,1);[1:n]']; v=matrix(v,1,2*n)
v=[zeros(1,n);[1:n]]; v=v([1:2*n])
v=[zeros(1,n);[1:n]]'; v=v([1:2*n])
v=[]; for i=1:n, v=[v,0,i]; end; v
v=[]; for i=1:n, v=[v,[0;i]]; end; v
v=kron([1:n],[0;1])
v=kron([1:n],[0,1])
v=[1:n]*[0:n-1]/2
v=[1:n].*[0:n-1]/2
v=[1:n]; v=v.*(v-1)/2
v=[1:n]; v=v.^2-v/2
v=[1:n]; v=(v.^2-v)/2
v=cumsum([1:n])
v=cumsum([0:n-1])
for i=1:n v(i)=i*(i-1)/2; end;
for i=1:n, v(i)=(i^2-i)/2; end; v
v=[]; for i=1:n, v=[v,i*(i-1)/2]; end;
x=sum(v*10^(-[1:length(v)]))
x=sum(v.*10^(-[1:length(v)]))
x=sum(v*10^(-[1:size(v)]))
x=sum(v.*10^(-[1:size(v,2)]))
x=sum(v.*10^(-[1:size(v,"*")]))
s="0"+"."+sum(string(v)); x=evstr(s)
s="0"+"."+strcat(string(v)); x=evstr(s)
x=0; for i=1:length(v), x=x+v(i)*10^(-i); end; x
x=0; for i=v, x=x+i*10^(-i); end; x
x=0; d=0.1; for i=v, d=d/10; x=x+i*d; end; x
x=0; d=0.1; for i=v, x=x+i*d; d=d/10; end; x
v=floor(x*10^[1:n])
v=floor(x*10^[1:n]); v=v-[0,v([1:n-1])]*10
v=[]; for i=1:n, a=int(x*10^i); v=[v,a]; end;
v=[]; for i=1:n, a=int(x*10); v=[v,a]; x=x*10-a; end; v
s=string(x); v=[]; for i=1:n, v=[v,part(s,i+2)]; end; v
s=string(x); v=[]; for i=1:n, v=[v,part(s,i+2)]; end; v=evstr(v)
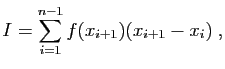
n=size(x,"*"); I = sum((x([2:n])-x([1:n-1]))*y([2:n]))
n=size(x,"*"); I = sum((x([2:n])-x([1:n-1])).*y([2:n]))
n=size(x,"*"); I = sum((x([2:n])-x([1:n-1]))*y([1:n-1]))
I=0; for i=1:length(x), I = I+(x(i+1)-x(i))*y(i+1); end; I
I=0; for i=2:length(x), I = I+(x(i)-x(i-1))*y(i); end; I
I=0; for i=1:length(x)-1, I = I+(x(i+1)-x(i))*y(i+1); end; I
t=argn(z)
t=phasemag(z)
t=%phasemag(z)/180*%pi
t=log(z/abs(z))/%i
t=imag(log(z/abs(z)))
t=imag(log(z/abs(z))); if imag(z)<0 then t=t+2*%pi; end; t
t=acos(real(z)/abs(z))
t=acos(real(z)/abs(z)); if imag(z)<0 then t=-t+2*%pi; end; t
t=asin(imag(z)/abs(z))
t=asin(imag(z)/abs(z)); if imag(z)<0 then t=-t+2%pi; end; t
t=atan(imag(z)/real(z))
Q=X^degree(P)*horner(P,1/X)
X=poly([0,1],"X","coeff"); Q=X^degree(P)*horner(P,1/X)
c=coeff(P); c=c([length(c):-1:1]); Q=poly(c,"X");
c=coeff(P); c=c([length(c):-1:1]); Q=poly(c,"X","coeff")
r=roots(P); Q=poly(1/r,"X")
r=roots(P); c=coeff(P); Q=c($)*poly((1)./r,"X")*prod(r)*(-1)^degree(P)
plot2d([0,1],[0,1],style=-5)
plot2d([0,1],[0,1],style=5)
x=[0:0.1:1]; plot2d(x,x,style=0)
x=[0:0.1:1]; plot2d2(x,x)
x=[0:0.1:1]; plot2d3(x,x)
x=[0,0.5;0.5,1]; plot2d(x,x)
x=[0,0.5;0.5,1]; plot2d(x,x,style=[5,5])
x=[-1;0;1]; y=[0;1;0]; plot2d([x,x],[y,-y],style=[1,1])
x=[-1,0,1]; y=[0,1,0]; plot2d([x;x],[y;-y],style=[1,1])
x=[0,1,0,-1]; y=[-1,0,1,0]; xpoly(x,y)
plot2d(0,0,rect=[-2,-2,2,2])
x=[0,1,0,-1]; y=[-1,0,1,0]; xpoly(x,y,"lines",1)
isoview(-1,1,-1,1).
Parmi les lignes de commande suivantes, lesquelles affichent
un cercle,
lesquelles ne l'affichent pas et pourquoi ?
x=linspace(-1,1,200)'; y=sqrt(1-x.^2);
plot2d([x,x],[y,-y],style=[5,5])
x=[-1:1]'; y=sqrt(1-x.^2); plot2d([x,x],[y,-y],style=[5,5])
x=linspace(-1,1,200)';y=sqrt(1-x.^2);plot2d([x;x],[y;-y],style=[5,5])
t=linspace(0,2*%pi); x=cos(t); y=sin(t); plot2d(x,y)
xarc(-1,1,2,2,0,2*%pi)
plot2d(0,0); xarc(-1,1,2,2,0,360*64)
e=0.1; x=linspace(e,%pi-e,200); y=(1)./sin(x);
plot2d(x,y,style=5,rect=[0,-10,2*%pi,10]);
e=0.1; x=linspace(%pi+e,2*%pi-e,200); y=(1)./sin(x);
plot2d(x,y,style=5,frameflag=0);
e=0.001; x=linspace(e,%pi-e,200); y=(1)./sin(x);
plot2d(x,y,style=5);
e=0.001; x=linspace(%pi+e,2*%pi-e,200); y=(1)./sin(x);
plot2d(x,y,style=5); e=0.1; x=linspace(e,%pi-e,200); x=[x',x'+%pi]; y=(1)./sin(x);
plot2d(x,y,style=[5,5]);
e=0.1; x=[e:e:%pi-e]; x=[x ,x+%pi]; y=(1)./sin(x);
plot2d(x,y,style=[5,5]);
x, et qui retourne la matrice des images des
coefficients de x par la fonction
deff("y=f(x)","y=1/(exp(x)*sin(x))")
deff("y=f(x)","y=(1)./(exp(x).*sin(x))")
deff("y=f(x)","y=1./(%e^x.*sin(x))")
deff("y=f(x)","y=(1)./(%e^x.*sin(x))")
deff("y=f(x)","y=exp(-x)./sin(x)")
function y=f(x) y=(1)./(%e^x.*sin(x)) endfunction
function y=f(x)
y=(1)./(%e^x.*sin(x))
endfunction
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales