Vrai ou faux

Vrai-Faux 1 Les lignes de commande suivantes affichent le vecteur ligne
[1] 1 2 3 4 5 : vrai ou faux et pourquoi ?

$\square\;$ (1,2,3,4,5)
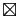
$\boxtimes\;$ c(1,2,3,4,5)
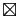
$\boxtimes\;$ 1:5
$\square\;$ 1,5
$\square\;$ rep(1,5)
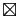
$\boxtimes\;$ seq(1,5)
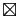
$\boxtimes\;$ cumsum(rep(1,5))
$\boxtimes\;$ which(rep(1,5)==1)
$\square\;$ which(rbin(5,1,1)<1)
$\boxtimes\;$ sort(sample(1:5,5))
$\boxtimes\;$ sort(seq(5,1,-1))
$\square\;$ for (i in 1:5){v[i] <- i}
$\boxtimes\;$ v <- rep(1,5); for (i in 1:5){v[i] <- i}; v
$\square\;$ v <- 1; for (i in 2:5){append(v,i)}; v
$\boxtimes\;$ v <- 1; for (i in 2:5){v <- append(v,i)}; v
$\boxtimes\;$ v <- 1; for (i in 2:5){v <- c(v,i)}; v
$\square\;$ v <- 1; for (i in 2:5){v <- rbind(v,i)}; v
$\square\;$ v <- rep(1,5); while (i<5){v[i] <- i}; v
$\boxtimes\;$ v<- 1; i<-1; while (i<5){i<-i+1; v[i] <- i}; v

Vrai-Faux 2 Les lignes de commande suivantes affichent le vecteur ligne
[1] 1 0.5 0.25 0.125 0.0625 : vrai ou faux et pourquoi ?

$\square\;$ 2^-0:4
$\square\;$ 2^(-0:4)
$\boxtimes\;$ 2^-(0:4)
$\square\;$ 2^(-(0:4))
$\square\;$ 1/2^0:4
$\boxtimes\;$ 1/2^(0:4)
$\square\;$ cumprod(rep(0.5,5))
$\boxtimes\;$ cumprod(c(1,rep(0.5,4)))
$\square\;$ v<-1; for (i in 1:4){v <- c(v,v/2)}; v
$\square\;$ v<-rep(1,5); for (i in 0:4){v(i) <- 2^(-i)}; v
$\square\;$ v<-1; for (i in 0:4){v[i] <- 1/2^i}; v
$\boxtimes\;$ v<-1; for (i in 2:4){v[i] <- 1/2^i}; v
$\square\;$ v<-1; while (v>0.1){v <- v/2}; v
$\square\;$ x<-1; v<-x; while(x>0.1){x<-x/2; v<-c(v,x)}; v

Vrai-Faux 3 Les lignes de commande suivantes affichent la matrice carrée dont la première ligne est le vecteur 0 1, la seconde ligne est le vecteur 1 0 : vrai ou faux et pourquoi ?

$\square\;$ [[0,1];[1,0]]
$\boxtimes\;$ rbind(c(0,1),c(1,0))
$\boxtimes\;$ cbind(0:1,1:0)
$\boxtimes\;$ matrix(c(0,1,1,0),2,2)
$\square\;$ matrix(rep(c(0,1),2),2,2)
$\square\;$ diag(rep(1,2))
$\boxtimes\;$ 1-diag(rep(1,2))
$\square\;$ v <- c(1,0); cbind(v,v)
$\boxtimes\;$ v <- c(1,0); rbind(sort(v),v)
$\boxtimes\;$ c(1,0)%*%t(c(0,1))+c(0,1)%*%t(c(1,0))
$\boxtimes\;$ 1:0%*%t(0:1)+0:1%*%t(1:0)
$\square\;$ 1:0*t(0:1)+0:1*t(1:0)
$\boxtimes\;$ toeplitz(c(0,1))
$\boxtimes\;$ toeplitz(0:1)

Vrai-Faux 4 Soit un entier. Les lignes de commande suivantes affichent le vecteur de longueur dont la coordonnée d'ordre vaut , les autres coordonnées étant nulles : vrai ou faux et pourquoi ?

$\boxtimes\;$ as.vector(rbind(rep(0,n),1:n))
$\square\;$ matrix(cbind(rep(0,n),1:n),1,2*n)
$\square\;$ matrix(rbind(rep(0,n),1:n),1,2*n)
$\boxtimes\;$ as.vector(matrix(rbind(rep(0,n),1:n),1,2*n))
$\square\;$ as.vector(matrix(rbind(1:n,rep(0,n)),2*n,1))
$\boxtimes\;$ as.vector(0:1%*%t(1:n))
$\square\;$ as.vector(1:n%*%t(1:0))
$\square\;$ as.vector(1:n%*%t(0:1))
$\square\;$ v<-0; for (i in 1:n){v[2*i]<-i}; v
$\boxtimes\;$ v<-rep(0,2*n); for (i in 1:n){v[2*i]<-i}; v
$\boxtimes\;$ v<-c(0,1); for (i in 2:n){v<-c(v,c(0,i))}; v
$\square\;$ v<-c(0,1); for (i in 2:n){v<-c(v,0:i)}; v

Vrai-Faux 5 Soit un entier. Les lignes de commande suivantes affichent le vecteur dont la coordonnée d'ordre vaut $\frac{i(i-1)}{2}$ , pour $i=1,\ldots,n$ : vrai ou faux, et pourquoi ?

$\square\;$ 1:n*0:n-1/2
$\boxtimes\;$ 1:n*0:(n-1)/2
$\boxtimes\;$ 1:n*seq(0,n-1)/2
$\square\;$ v<-1:n; v^2-v/2
$\boxtimes\;$ v<-1:n; (v^2-v)/2
$\square\;$ v<-1:n; v%*%(v-1)/2
$\square\;$ cumsum(0:n-1)
$\boxtimes\;$ cumsum(0:(n-1))
$\boxtimes\;$ cumsum(seq(0,n-1))
$\square\;$ v<-rep(0,n); for (i in 1:n){v(i)<-i*(i-1)/2}; v
$\boxtimes\;$ v<-rep(0,n); for (i in 1:n){v[i]<-i*(i-1)/2}; v
$\boxtimes\;$ v<-0; for (i in 2:n){v<-c(v,i*(i-1)/2)}; v

Vrai-Faux 6 Soit un entier et $v=(v_1,\ldots,v_n)$ un vecteur d'entiers, tous compris entre 0 et . Les lignes de commande suivantes affichent le réel compris entre 0 et dont les décimales sont $v_1,\ldots,v_n$ : vrai ou faux et pourquoi ?

$\square\;$ sum(v*10^-1:length(v))
$\boxtimes\;$ sum(v*10^-(1:length(v)))
$\boxtimes\;$ sum(v%*%10^-(1:length(v)))
$\square\;$ paste("0",".",v)
$\square\;$ paste(c("0",".",v))
$\square\;$ paste(c("0",".",v),collapse='')
$\boxtimes\;$ as.numeric(paste(c("0",".",v),collapse=''))
$\boxtimes\;$ x<-0; d<-0.1; for (i in v){x<-x+d*i; d<-d/10}; x
$\square\;$ x<-0; for (i in v){x<-x+i*10^(-i)}; x

Vrai-Faux 7 Soit un vecteur d'entiers tous compris entre et . Les lignes de commande suivantes affectent à v un vecteur de taille , contenant les fréquences empiriques des entiers entre et : vrai ou faux et pourquoi ?

$\square\;$ v<-table(x)/length(x)
$\square\;$ v<-table(factor(x,levels=1:5))/length(x)
$\boxtimes\;$ v<-as.vector(table(factor(x,levels=1:5))); v/sum(v)
$\square\;$ v<-rep(1,5); for (i in 1:5){v[i]<-which(x=i)}; v/sum(v)
$\square\;$ v<-rep(1,5); for (i in 1:5){v[i]<-length(which(x==i))}; v/sum(v)

Vrai-Faux 8 Soit un vecteur numérique. Les lignes de commande suivantes retournent la moyenne de : vrai ou faux et pourquoi ?

$\boxtimes\;$ mean(x)
$\boxtimes\;$ sum(x)/length(x)
$\square\;$ mean(table(x))
$\square\;$ mean(as.vector(table(x))

$\boxtimes\;$

t <- table(x); 
sum(as.numeric(row.names(t))*as.vector(t))/length(x)

Vrai-Faux 9 Soit un vecteur numérique. Les lignes de commande suivantes retournent une médiane de : vrai ou faux et pourquoi ?

$\boxtimes\;$ median(x)
$\square\;$ quantile(x,0.5)
$\boxtimes\;$ as.numeric(quantile(x,0.5))
$\boxtimes\;$ as.vector(quantile(x,0.5))
$\square\;$ x[length(x)/2]
$\square\;$ sort(x)(round(length(x))/2)
$\boxtimes\;$ sort(x)[floor(length(x)/2)]

Vrai-Faux 10 Soit un entier. Les lignes de commande suivantes retournent un échantillon de taille de la loi de Bernoulli de paramètre : vrai ou faux et pourquoi ?

$\square\;$ rbernoul(n,0.5)
$\square\;$ rbinom(n,0.5)
$\boxtimes\;$ rbinom(n,1,0.5)
$\square\;$ runif(n,0,1)
$\boxtimes\;$ floor(runif(n,0,2))
$\boxtimes\;$ round(runif(n,0,1))
$\square\;$ ceiling(runif(n,0,2))
$\boxtimes\;$ ceiling(runif(n,0,2))-1
$\boxtimes\;$ (1+sign(rnorm(10)))/2
$\boxtimes\;$ (1+sign(rnorm(10,0,2)))/2
$\square\;$ (1+sign(rnorm(10,2,0)))/2
$\boxtimes\;$ ifelse(rnorm(n)<0,yes=0,no=1)
$\square\;$ ifelse(runif(n,0,2)<0.5,yes=0,no=1)
$\boxtimes\;$ rep(0,n); v[which(runif(n,0,1)<0.5)]=1
$\square\;$ rep(n,0); v[which(runif(n,0,1)<0.5)]=1
$\boxtimes\;$ ifelse(rgeom(n,0.5)>0,yes=1)
$\boxtimes\;$ ifelse(rgeom(n,0.5)>0,yes=0,no=1)
$\square\;$ sample(n,c(0,1))
$\square\;$ sample(c(0,1),n)
$\boxtimes\;$ sample(c(0,1),n,replace=TRUE)

Vrai-Faux 11 Les lignes de commande suivantes retournent 0 : vrai ou faux et pourquoi ?

$\boxtimes\;$ qnorm(0.5)
$\square\;$ qnorm(0.5,0.5)
$\boxtimes\;$ dnorm(100)
$\square\;$ pnorm(0.5)
$\boxtimes\;$ pbinom(1,1,0,lower=F)
$\square\;$ dbinom(1,1,1)
$\boxtimes\;$ dbinom(2,1,0.5)
$\boxtimes\;$ ppois(0,1000)
$\square\;$ qgeom(0.6,0.5)
$\boxtimes\;$ qgeom(0.4,0.5)
$\boxtimes\;$ qt(0.5,3)
$\square\;$ qchisq(0.5,3)

Vrai-Faux 12 Soit un échantillon de taille d'une loi d'espérance $\mu$ inconnue. Les lignes de commande suivantes retournent un vecteur à deux entrées dont les composantes sont les bornes d'un intervalle de confiance de niveau asymptotique pour $\mu$ : vrai ou faux et pourquoi ?

$\square\;$ t.test(x)$conf.int
$\boxtimes\;$ as.vector(t.test(x)$conf.int)
$\square\;$ mean(x)+sd(x)*qnorm(0.975)*c(-1,1)
$\boxtimes\;$ mean(x)+sd(x)*qnorm(0.975)*c(-1,1)/sqrt(length(x))
$\square\;$ mean(x)+sd(x)*qnorm(0.025,0.975)/sqrt(length(x))
$\square\;$ mean(x)+sd(x)*qnorm(c(0.025,0.975))/sqrt(length(x))

Vrai-Faux 13 Soit un échantillon de taille d'une loi d'espérance $\mu$ inconnue. Les lignes de commande suivantes retournent la p-valeur d'un test unilatéral de $\mathcal{H}_0$ : $\mu=0$ contre $\mathcal{H}_1$ : $\mu>0$ : vrai ou faux et pourquoi ?

$\square\;$ t.test(x)$p.value
$\boxtimes\;$ t.test(x,alternative="greater")$p.value
$\square\;$ pnorm(mean(x)/sd(x))
$\square\;$ pnorm(sqrt(length(x))*mean(x)/sd(x))
$\boxtimes\;$ 1-pnorm(sqrt(length(x))*mean(x)/sd(x))
$\boxtimes\;$ pnorm(sqrt(length(x))*mean(x)/sd(x),lower.tail=F)