Commençons par rappeler deux résultats fondamentaux que vous
connaissez déjà par c ur (si ce n'est pas le cas,
dépêchez-vous de les apprendre).
ur (si ce n'est pas le cas,
dépêchez-vous de les apprendre).
Théorème 1
- Pour tout
![$ x\in ]-1,1[$](img7.gif) :
:
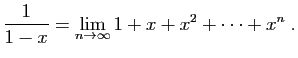 |
(1) |
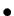
- Pour tout
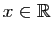 :
:
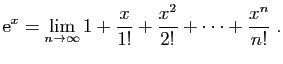 |
(2) |
Le premier s'obtient à partir de l'identité :
Le second se déduit de la formule du binôme de Newton et est
démontré dans le chapitre sur les fonctions usuelles.
Il faut voir dans (1) et (2) des résultats
d'approximation : ils permettent d'évaluer de manière
relativement précise la valeur prise par une fonction, en
calculant un polynôme (ce qui est non seulement facile à
la main, mais surtout peu coûteux en temps de calcul).
À ce propos, dans tout le chapitre nous commettons
l'abus de langage consistant à désigner par «polynôme»
ce qui est en fait une fonction polynomiale.
Considérons la formule (1). Notons :
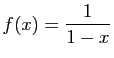
et
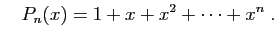
La figure 1 montre une représentation graphique de
la fonction 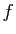 et des polynômes
et des polynômes 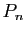 pour
pour 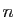 allant de 0 à
allant de 0 à 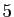 . Plus
. Plus 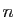 est grand, meilleure est
l'approximation pour un
est grand, meilleure est
l'approximation pour un 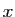 donné. Dans ce cas particulier, il est
facile de calculer l'erreur commise si on remplace
donné. Dans ce cas particulier, il est
facile de calculer l'erreur commise si on remplace 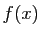 par
par
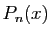 .
.
Cette erreur est donc de l'ordre de 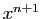 . Pour être plus
concret, pensez
. Pour être plus
concret, pensez 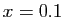 . Alors
. Alors
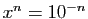 et
et
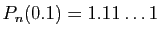 .
La différence
.
La différence
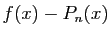 vaut
vaut
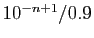 . Pour
. Pour 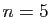 , on
commet une erreur de l'ordre du millionième en remplaçant
, on
commet une erreur de l'ordre du millionième en remplaçant
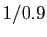 par
par 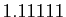 .
.
Figure:
Fonction
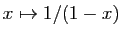 et ses polynômes de Taylor en
0 jusqu'à l'ordre
et ses polynômes de Taylor en
0 jusqu'à l'ordre 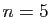 .
.
|
|
L'intérêt est plus flagrant pour l'exponentielle, pour
laquelle il n'existe pas d'autre moyen de calcul que de l'approcher
par des polynômes. Posons :
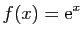
et
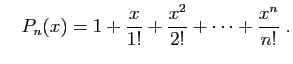
Le tableau ci-dessous donne la différence entre 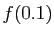 et
et 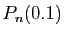 ,
pour
,
pour 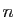 allant de 0 à
allant de 0 à 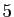 (voir la figure 2 pour la
représentation graphique de
(voir la figure 2 pour la
représentation graphique de 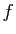 et
et
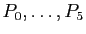 ).
).
Figure:
Fonction
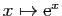 et ses polynômes de Taylor en
0 jusqu'à l'ordre
et ses polynômes de Taylor en
0 jusqu'à l'ordre 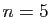 .
.
|
|
Comment obtient-on les polynômes 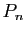 à partir de
à partir de 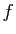 ? C'est
très simple : on fait en sorte que leurs dérivées en 0 coïncident avec celles de la fonction jusqu'à l'ordre
? C'est
très simple : on fait en sorte que leurs dérivées en 0 coïncident avec celles de la fonction jusqu'à l'ordre 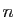 :
:
Le polynôme 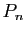 étant de degré
étant de degré 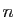 , il est entièrement
déterminé par la donnée de ses
, il est entièrement
déterminé par la donnée de ses 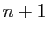 coefficients :
coefficients :
Vérifiez sur les deux exemples ci-dessus : la dérivée 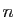 -ième
en 0 de
-ième
en 0 de
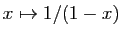 est
est 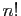 , celle de
, celle de
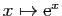 est
est 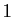 .
Ce que nous venons de voir au voisinage de 0, s'étend en
n'importe quel point de la façon suivante.
.
Ce que nous venons de voir au voisinage de 0, s'étend en
n'importe quel point de la façon suivante.
L'idée est de remplacer une fonction 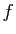 que l'on ne sait pas
calculer (ou difficilement) par un polynôme, qui est facilement
calculable. Mais si
que l'on ne sait pas
calculer (ou difficilement) par un polynôme, qui est facilement
calculable. Mais si 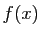 n'est pas calculable, alors bien sûr le
reste
n'est pas calculable, alors bien sûr le
reste 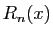 ne l'est pas non plus. On doit donc chercher des moyens
d'estimer ou de majorer ce reste. Nous les étudierons à la section
suivante. Le moins que l'on puisse demander quand on approche une
fonction par un polynôme de degré
ne l'est pas non plus. On doit donc chercher des moyens
d'estimer ou de majorer ce reste. Nous les étudierons à la section
suivante. Le moins que l'on puisse demander quand on approche une
fonction par un polynôme de degré 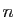 , est que
le reste soit négligeable devant
, est que
le reste soit négligeable devant 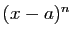 .
C'est le sens de la définition suivante.
.
C'est le sens de la définition suivante.
Nous verrons que toutes les fonctions usuelles admettent un
développement limité pour lequel 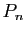 est le polynôme de
Taylor. Même si on ne les utilise jamais, il existe des fonctions
qui ne vérifient pas les hypothèses de la définition
1 et qui pourtant admettent des développements
limités. Par exemple la fonction
est le polynôme de
Taylor. Même si on ne les utilise jamais, il existe des fonctions
qui ne vérifient pas les hypothèses de la définition
1 et qui pourtant admettent des développements
limités. Par exemple la fonction 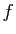 définie par :
définie par :
Elle vérifie évidemment
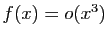 , elle admet donc des
développements limités en 0 d'ordre
, elle admet donc des
développements limités en 0 d'ordre 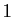 ,
, 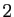 et
et 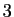 . Pourtant elle
n'est continue sur aucun intervalle contenant 0.
Nous nous ramènerons toujours à des
développements limités au voisinage de 0, grâce à
l'observation suivante.
. Pourtant elle
n'est continue sur aucun intervalle contenant 0.
Nous nous ramènerons toujours à des
développements limités au voisinage de 0, grâce à
l'observation suivante.
Désormais, nous simplifierons les écritures en n'écrivant
plus que des développements limités en 0.
Un développement limité, s'il existe, est
unique au sens suivant.
Démonstration : Le polynôme 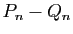 est de degré au plus
est de degré au plus 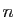 , et il est
négligeable devant
, et il est
négligeable devant 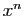 au voisinage de 0. Ce n'est possible
que s'il est nul.
au voisinage de 0. Ce n'est possible
que s'il est nul.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![$ x\in ]-1,1[$](img7.gif) :
:
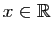 :
:
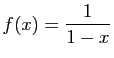 et
et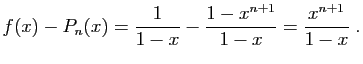
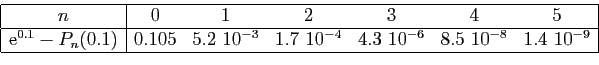
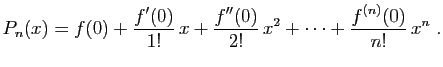
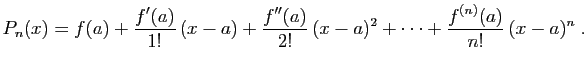
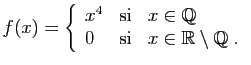
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales