... dans le cercle, le diamètre est à la circonférence commeEn écriture moderne :à
. J'ai reçu cette série (parmi d'autres pour le même but, et tirées du même principe), de l'excellent analyste, et mon ami très estimé, Mr John Machin.
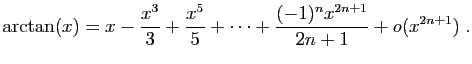
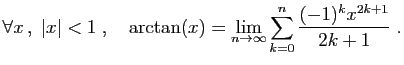
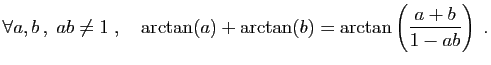
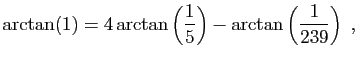
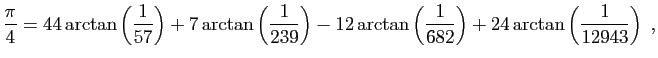
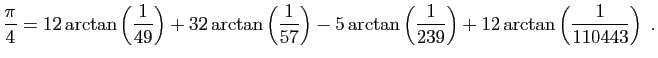
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales