Vous savez sans doute déjà qu'en géométrie plane, l'aire d'un
parallélogramme est au signe près le déterminant des deux vecteurs qui
l'engendrent. C'est vrai en dimension quelconque.
En dimension 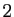 , c'est un parallélogramme, en dimension
, c'est un parallélogramme, en dimension 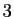 un
parallélépipède ordinaire (figure 2).
un
parallélépipède ordinaire (figure 2).
Figure 2:
Parallélépipèdes en dimension 2 et 3.
|
|
Pour définir une mesure, il faut un étalon qui en donne
l'unité. Dans
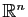 , on convient que
le volume du parallélépipède engendré par les vecteurs de la
base canonique est
, on convient que
le volume du parallélépipède engendré par les vecteurs de la
base canonique est 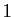 . Dans un espace vectoriel
. Dans un espace vectoriel 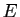 , on peut
choisir une base
, on peut
choisir une base 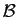 quelconque, et décider que le volume du parallélépipède
qu'elle engendre vaut
quelconque, et décider que le volume du parallélépipède
qu'elle engendre vaut
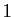 .
.
Une fois fixé l'étalon, comment calculer le volume des autres
parallélépipèdes, c'est-à-dire définir une application 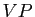 qui à un
qui à un 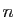 -uplet
-uplet
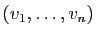 associe le volume du
parallélépipède
associe le volume du
parallélépipède
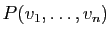 ?
?
Voici trois propriétés «physiquement
raisonnables».
- (P1)
- Si on remplace un vecteur par la somme de deux autres, le
volume est la somme des deux volumes.
- (P2)
- Si on multiplie un des vecteurs par un réel, le volume
doit être multiplié par ce même réel.
- (P3)
- Si deux des vecteurs sont identiques, alors le volume est
nul.
La propriété (P1) est facile à admettre. Pensez à deux
boîtes posées l'une sur l'autre : elles ont une face en commun et
la pile forme un nouveau parallélépipède, dont le volume est
bien la somme des volumes des deux boîtes. Attention, si vous
l'admettez pour 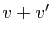 , vous devez l'admettre aussi pour
, vous devez l'admettre aussi pour 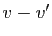 ; et si
on peut soustraire deux volumes, alors un volume peut être
négatif. Effectivement, le volume ici est muni d'un signe. La valeur
absolue est la mesure au sens ordinaire, le signe traduit
l'orientation du
; et si
on peut soustraire deux volumes, alors un volume peut être
négatif. Effectivement, le volume ici est muni d'un signe. La valeur
absolue est la mesure au sens ordinaire, le signe traduit
l'orientation du 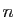 -uplet de vecteurs.
La propriété (P2) est elle aussi assez naturelle :
si vous étirez un parallélépipède dans
une direction, vous multipliez son volume. Mais surtout, elle est
(presque) une conséquence de (P1) : en effet, pour tout
-uplet de vecteurs.
La propriété (P2) est elle aussi assez naturelle :
si vous étirez un parallélépipède dans
une direction, vous multipliez son volume. Mais surtout, elle est
(presque) une conséquence de (P1) : en effet, pour tout 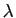 entier, puis rationnel, (P2) se déduit de
(P1). Il suffit alors
de faire l'hypothèse que les applications partielles sont continues
au voisinage de 0 pour en déduire la propriété pour tout
entier, puis rationnel, (P2) se déduit de
(P1). Il suffit alors
de faire l'hypothèse que les applications partielles sont continues
au voisinage de 0 pour en déduire la propriété pour tout
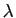 réel. La propriété (P3) est aussi très
naturelle : si deux des vecteurs qui engendrent le
parallélépipède sont identiques,
celui-ci est «aplati», c'est-à-dire qu'il est inclus dans un
hyperplan. Étant inclus dans un sous-espace de dimension
inférieure, son volume
réel. La propriété (P3) est aussi très
naturelle : si deux des vecteurs qui engendrent le
parallélépipède sont identiques,
celui-ci est «aplati», c'est-à-dire qu'il est inclus dans un
hyperplan. Étant inclus dans un sous-espace de dimension
inférieure, son volume 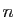 -dimensionnel est nul.
-dimensionnel est nul.
Maintenant, relisez la section 1.2, en particulier
la définition 6
et la proposition 3. L'application
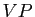 , si elle vérifie les propriétés (P1), (P2) et (P3), est une
forme multilinéaire alternée. Si
de plus
, si elle vérifie les propriétés (P1), (P2) et (P3), est une
forme multilinéaire alternée. Si
de plus
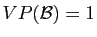 , alors
, alors 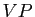 est le déterminant dans la base
est le déterminant dans la base
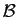 .
Si
.
Si
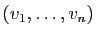 est tel que
det
est tel que
det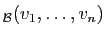 est non nul, alors
est non nul, alors
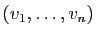 est une
base de
est une
base de 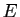 . La valeur absolue du déterminant est le volume du
parallélépipède engendré, au sens
ordinaire. Son signe est positif si la nouvelle base a la même
orientation que l'ancienne, négatif dans le cas contraire.
. La valeur absolue du déterminant est le volume du
parallélépipède engendré, au sens
ordinaire. Son signe est positif si la nouvelle base a la même
orientation que l'ancienne, négatif dans le cas contraire.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() , on convient que
le volume du parallélépipède engendré par les vecteurs de la
base canonique est
, on convient que
le volume du parallélépipède engendré par les vecteurs de la
base canonique est ![]() . Dans un espace vectoriel
. Dans un espace vectoriel ![]() , on peut
choisir une base
, on peut
choisir une base ![]() quelconque, et décider que le volume du parallélépipède
qu'elle engendre vaut
quelconque, et décider que le volume du parallélépipède
qu'elle engendre vaut
![]() .
.
![]() qui à un
qui à un ![]() -uplet
-uplet
![]() associe le volume du
parallélépipède
associe le volume du
parallélépipède
![]() ?
?
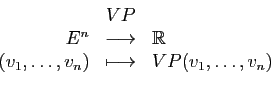
![]() , si elle vérifie les propriétés (P1), (P2) et (P3), est une
forme multilinéaire alternée. Si
de plus
, si elle vérifie les propriétés (P1), (P2) et (P3), est une
forme multilinéaire alternée. Si
de plus
![]() , alors
, alors ![]() est le déterminant dans la base
est le déterminant dans la base
![]() .
Si
.
Si
![]() est tel que
det
est tel que
det![]() est non nul, alors
est non nul, alors
![]() est une
base de
est une
base de ![]() . La valeur absolue du déterminant est le volume du
parallélépipède engendré, au sens
ordinaire. Son signe est positif si la nouvelle base a la même
orientation que l'ancienne, négatif dans le cas contraire.
. La valeur absolue du déterminant est le volume du
parallélépipède engendré, au sens
ordinaire. Son signe est positif si la nouvelle base a la même
orientation que l'ancienne, négatif dans le cas contraire.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales