L'ensemble
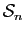 des permutations de l'ensemble
des permutations de l'ensemble
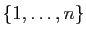 , muni de la
composition des applications est le premier exemple de
groupe non commutatif que vous ayez rencontré. Vous avez besoin d'en
savoir un peu plus pour manipuler des déterminants. La notion
importante de cette section est celle de signature.
Soit
, muni de la
composition des applications est le premier exemple de
groupe non commutatif que vous ayez rencontré. Vous avez besoin d'en
savoir un peu plus pour manipuler des déterminants. La notion
importante de cette section est celle de signature.
Soit
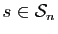 une bijection de
une bijection de
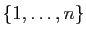 dans
lui-même. Nous la noterons
dans
lui-même. Nous la noterons
Par exemple pour 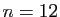 :
:
est la bijection qui à 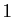 associe
associe 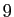 , à
, à 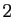 associe
associe 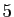 , etc. On
peut se demander pourquoi imposer une notation aussi redondante,
puisque les images sont données par la deuxième ligne dans l'ordre
de la première. La raison est que l'on réserve une notation plus
simple aux cycles. La composition des applications est notée
, etc. On
peut se demander pourquoi imposer une notation aussi redondante,
puisque les images sont données par la deuxième ligne dans l'ordre
de la première. La raison est que l'on réserve une notation plus
simple aux cycles. La composition des applications est notée
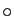 , mais nous noterons
, mais nous noterons 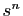 la composée de
la composée de  avec
elle-même
avec
elle-même 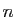 fois.
fois.
Définition 1
Soit  une permutation de
une permutation de
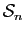 et
et 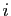 un élément de
un élément de
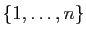 .
On appelle orbite de
.
On appelle orbite de 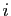 pour
pour  l'ensemble (fini)
l'ensemble (fini)
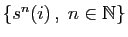 .
.
Dans l'exemple ci-dessus, pour trouver l'orbite de 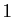 , on calcule
l'image de
, on calcule
l'image de 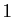 qui est
qui est 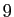 , puis l'image de
, puis l'image de 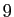 qui est
qui est 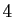 ,
etc., jusqu'à retrouver
,
etc., jusqu'à retrouver 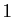 (qui est l'image de
(qui est l'image de 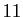 ). L'orbite de
). L'orbite de 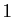 est donc
est donc
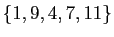 .
L'orbite de
.
L'orbite de 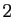 est
est 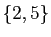 , celle de
, celle de 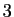 est
est 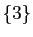 (on dit que
(on dit que 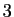 est un point fixe). Observez qu'une orbite est la même pour tous
ses éléments : l'orbite de
est un point fixe). Observez qu'une orbite est la même pour tous
ses éléments : l'orbite de 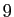 ,
, 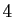 ,
, 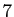 et
et 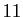 est aussi
est aussi
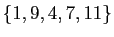 . Le plus petit entier
. Le plus petit entier 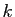 tel que
tel que 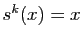 est la
longueur de l'orbite
est la
longueur de l'orbite
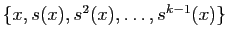 .
Par définition, un ensemble n'est pas ordonné. Or nous aurons
besoin d'un ordre pour écrire des cycles. Nous conviendrons
donc d'écrire une orbite comme la liste ordonnée
.
Par définition, un ensemble n'est pas ordonné. Or nous aurons
besoin d'un ordre pour écrire des cycles. Nous conviendrons
donc d'écrire une orbite comme la liste ordonnée
![$ [x,s(x),\ldots,
s^{k-1}(x)]$](img27.gif) , où
, où 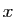 est le plus petit élément de l'orbite.
est le plus petit élément de l'orbite.
Définition 2
On appelle décomposition en orbites de la permutation  la séquence d'orbites disjointes des éléments de
la séquence d'orbites disjointes des éléments de
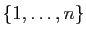 pour
pour  , écrite par ordre croissant de leurs plus petits éléments.
, écrite par ordre croissant de leurs plus petits éléments.
Un algorithme très simple produit la décomposition en orbites
d'une permutation.
Tant qu'il reste des éléments de
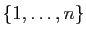 hors des orbites
déjà écrites
hors des orbites
déjà écrites
choisir le plus petit de ces éléments
écrire son orbite
Fin Tant que
Dans l'exemple ci-dessus, on commencera donc par écrire l'orbite de
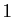 :
:
![$ [1,9,4,7,11]$](img29.gif) . Le premier élément non rangé est
. Le premier élément non rangé est 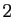 . Son
orbite est
. Son
orbite est ![$ [2,5]$](img30.gif) . L'élément
. L'élément 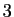 n'a pas été rangé, son orbite
est
n'a pas été rangé, son orbite
est ![$ [3]$](img31.gif) . Le plus petit élément non rangé à ce stade est
. Le plus petit élément non rangé à ce stade est 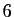 ,
dont l'orbite est
,
dont l'orbite est
![$ [6,12,8,10]$](img33.gif) . Tous les éléments
ont alors été rangés,
et la décomposition en orbites de
. Tous les éléments
ont alors été rangés,
et la décomposition en orbites de  est :
est :
Définition 3
Soit
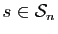 une permutation et
une permutation et
sa décomposition en orbites.
On appelle signature de la
permutation  et on note
et on note
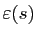 :
:
où
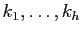 sont les longueurs des orbites successives dans la
décomposition de
sont les longueurs des orbites successives dans la
décomposition de  .
.
Toujours sur le même exemple, les longueurs des orbites successives
sont 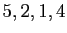 , la signature est donc
, la signature est donc
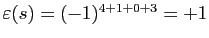 .
Soyons honnêtes : sachant décomposer une permutation en orbites
et en déduire sa signature, vous en savez assez pour calculer
des déterminants, ce qui après tout est bien le but de ce
chapitre. Il serait dommage de vous en tenir là, car vous
perdriez le sel algébrique du groupe des permutations.
Voici le résultat principal de cette section.
.
Soyons honnêtes : sachant décomposer une permutation en orbites
et en déduire sa signature, vous en savez assez pour calculer
des déterminants, ce qui après tout est bien le but de ce
chapitre. Il serait dommage de vous en tenir là, car vous
perdriez le sel algébrique du groupe des permutations.
Voici le résultat principal de cette section.
Théorème 1
L'application signature, de
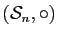 dans
dans
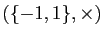 est l'unique homomorphisme surjectif entre ces deux groupes.
est l'unique homomorphisme surjectif entre ces deux groupes.
La démonstration comporte plusieurs étapes, qui sont autant de
résultats intéressants. D'abord, nous allons enrichir
les orbites pour donner un sens plus précis
à la notion de décomposition.
L'inconvénient de cette notation est que plusieurs écritures
différentes peuvent désigner le même cycle : 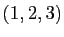 et
et
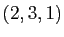 par exemple. Comme ci-dessus, nous convenons d'écrire
en premier le plus petit élément du cycle. Ceci permet d'associer de
manière unique un cycle à une orbite.
Observez que dans la décomposition en orbites du cycle
par exemple. Comme ci-dessus, nous convenons d'écrire
en premier le plus petit élément du cycle. Ceci permet d'associer de
manière unique un cycle à une orbite.
Observez que dans la décomposition en orbites du cycle
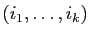 on trouve
on trouve
![$ [i_1,\ldots,i_k]$](img51.gif) , et
, et 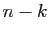 points fixes. La signature du cycle
points fixes. La signature du cycle
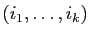 est :
est :
Proposition 1
Soit  une permutation et
une permutation et
sa décomposition en orbites. Alors  est la composée des cycles
déduits des orbites de longueur
est la composée des cycles
déduits des orbites de longueur
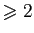 .
.
La vérification est immédiate.
Observez que deux cycles commutent si
les ensembles d'éléments qu'ils
concernent sont disjoints :
Dans une décomposition en orbites,
oubliez les singletons et ne conservez
que les orbites de longueur au moins 2, que vous transformez en
cycles : si
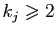 , remplacez
, remplacez
![$ [i_j,\ldots,s^{k_j-1}(i_j)]$](img58.gif) par
par
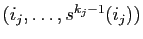 . Enfin,
remplacez les virgules dans l'énumération des orbites, par le signe de
composition :
votre permutation
. Enfin,
remplacez les virgules dans l'énumération des orbites, par le signe de
composition :
votre permutation  est une composée de cycles.
est une composée de cycles.
Les cycles de longueur 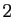 jouent un rôle particulier. On les
appelle transpositions. Leur signature vaut
jouent un rôle particulier. On les
appelle transpositions. Leur signature vaut  .
Afin de faciliter la lecture, pour
.
Afin de faciliter la lecture, pour
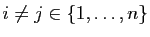 nous noterons
nous noterons
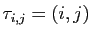 la
transposition de
la
transposition de 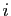 et
et 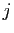 :
:
Proposition 2
Soit  une permutation et
une permutation et
sa décomposition en orbites. Alors  est la composée de
est la composée de
 transpositions.
transpositions.
Remarquez que le nombre de transpositions dans cette décomposition
est exactement l'exposant de 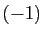 dans la définition de la signature.
Démonstration : Nous avons vu (proposition 1) que toute
permutation s'écrit comme une composée de cycles.
Il nous suffit de vérifier qu'un cycle de longueur
dans la définition de la signature.
Démonstration : Nous avons vu (proposition 1) que toute
permutation s'écrit comme une composée de cycles.
Il nous suffit de vérifier qu'un cycle de longueur 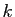 est composée de
est composée de
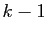 transpositions.
Voici une manière de décomposer le cycle
transpositions.
Voici une manière de décomposer le cycle
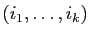 :
:
(vérifiez-le, par récurrence sur 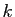 ).
). Toute permutation s'écrit donc comme un
produit (au sens de la composition des applications) de
transpositions. Une telle écriture n'a rien d'unique :
l'ordre de deux cycles disjoints peut être changé,
on peut toujours insérer deux fois la même
permutation dans le produit sans changer le résultat, etc.
Le miracle est que si deux
produits de transpositions donnent la même permutation, alors les
nombres de permutations dans ces deux produits ont la même
parité : c'est une conséquence du théorème
1. Le résultat suivant est l'étape
clé dans sa démonstration.
Toute permutation s'écrit donc comme un
produit (au sens de la composition des applications) de
transpositions. Une telle écriture n'a rien d'unique :
l'ordre de deux cycles disjoints peut être changé,
on peut toujours insérer deux fois la même
permutation dans le produit sans changer le résultat, etc.
Le miracle est que si deux
produits de transpositions donnent la même permutation, alors les
nombres de permutations dans ces deux produits ont la même
parité : c'est une conséquence du théorème
1. Le résultat suivant est l'étape
clé dans sa démonstration.
Lemme 1
Soit  une permutation et
une permutation et 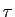 une transposition. Alors :
une transposition. Alors :
Démonstration : L'idée de la démonstration est de montrer que la composée par une
transposition agit sur la décomposition en orbites, soit en cassant
une orbite en deux, soit en regroupant deux orbites. Dans les deux cas
l'exposant de la signature est soit augmenté, soit
diminué de 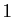 , et
la signature est changée en son opposée.
Considérons la décomposition en orbites de
, et
la signature est changée en son opposée.
Considérons la décomposition en orbites de  .
Supposons que
.
Supposons que 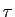 transpose les deux éléments distincts
transpose les deux éléments distincts 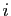 et
et 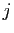 et
examinons la décomposition en orbites de
et
examinons la décomposition en orbites de
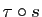 .
De deux choses l'une : soit
.
De deux choses l'une : soit 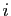 et
et 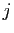 appartiennent à la même
orbite de
appartiennent à la même
orbite de  ,
soit
,
soit 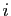 et
et 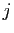 appartiennent à deux orbites distinctes.
appartiennent à deux orbites distinctes.
- Si
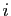 et
et 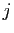 appartiennent à la même
orbite de
appartiennent à la même
orbite de  . Quitte à réordonner les éléments, nous pouvons
supposer sans perte de généralité que l'orbite est
. Quitte à réordonner les éléments, nous pouvons
supposer sans perte de généralité que l'orbite est
![$ [1,\ldots,k]$](img75.gif) , et que les deux éléments à transposer sont
, et que les deux éléments à transposer sont
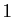 et
et 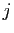 avec
avec
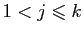 . Pour la permutation
. Pour la permutation
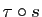 , l'image d'un entier
, l'image d'un entier 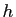 est :
est :
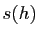 si
si 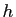 est différent de
est différent de 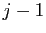 et
et 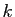 ,
,
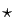
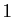 si
si 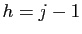 ,
,
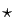
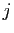 si
si 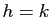 .
.
L'orbite
![$ [1,\ldots,k]$](img75.gif) est cassée en
est cassée en
![$ [1,\ldots,j-1]$](img83.gif) et
et
![$ [j,\ldots,k]$](img84.gif) . Le terme
. Le terme 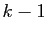 dans l'exposant de la signature
est remplacé par
dans l'exposant de la signature
est remplacé par
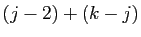 . L'exposant de la
signature est diminué de
. L'exposant de la
signature est diminué de 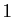 , et celle-ci est changée en son
opposée.
, et celle-ci est changée en son
opposée.
- Si
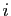 et
et 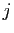 appartiennent à deux orbites
distinctes de
appartiennent à deux orbites
distinctes de  . Quitte à réordonner les éléments, nous
pouvons supposer sans perte de généralité que les deux orbites
sont
. Quitte à réordonner les éléments, nous
pouvons supposer sans perte de généralité que les deux orbites
sont
![$ [1,\ldots,j-1]$](img83.gif) et
et
![$ [j,\ldots,k]$](img84.gif) , avec
, avec
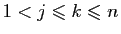 et que les deux éléments à transposer sont
et que les deux éléments à transposer sont 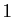 et
et 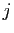 . Pour la permutation
. Pour la permutation
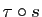 , l'image d'un
entier
, l'image d'un
entier 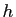 est :
est :
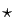
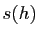 si
si 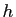 est différent de
est différent de 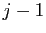 et
et 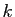
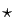
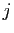 si
si 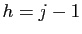
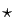
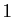 si
si 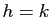
Les deux orbites
![$ [1,\ldots,j-1]$](img83.gif) et
et
![$ [j,\ldots,k]$](img84.gif) sont
regroupées en une seule :
sont
regroupées en une seule :
![$ [1,\dots,k]$](img87.gif) . Les deux termes
. Les deux termes 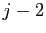 et
et
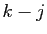 dans l'exposant de la signature sont remplacés par le terme
dans l'exposant de la signature sont remplacés par le terme
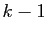 . L'exposant de la signature est augmenté de
. L'exposant de la signature est augmenté de 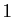 , et celle-ci
est encore changée en son opposée.
, et celle-ci
est encore changée en son opposée.
 Nous avons maintenant tous les outils pour démontrer le théorème
1.
Démonstration : Nous commençons par démontrer que la signature est un
homomorphisme de groupes, de
Nous avons maintenant tous les outils pour démontrer le théorème
1.
Démonstration : Nous commençons par démontrer que la signature est un
homomorphisme de groupes, de
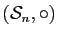 dans
dans
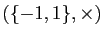 :
:
Soient  et
et 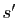 deux transpositions quelconques.
D'après la proposition 2,
deux transpositions quelconques.
D'après la proposition 2,
 est le produit de
est le produit de
 transpositions, où
transpositions, où
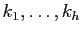 sont les longueurs des orbites de
sont les longueurs des orbites de  . Or d'après
le lemme 1, la composée d'une
transposition par une permutation quelconque mutiplie sa signature par
. Or d'après
le lemme 1, la composée d'une
transposition par une permutation quelconque mutiplie sa signature par
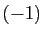 . La composée de
. La composée de 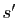 par
par
 transpositions successives
multiplie la signature par
transpositions successives
multiplie la signature par
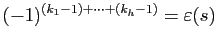 , d'où le résultat.
, d'où le résultat.
Pour terminer la démonstration du théorème
1, nous devons démontrer l'unicité.
Soit  une permutation quelconque : multiplions la transposition
une permutation quelconque : multiplions la transposition
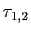 à droite par
à droite par 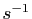 et à gauche par
et à gauche par  : on
obtient la transposition
: on
obtient la transposition
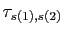 . N'importe quelle
transposition se déduit donc de
. N'importe quelle
transposition se déduit donc de
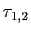 par une opération de
ce type (on dit que les transpositions sont toutes conjuguées).
Considérons maintenant un homomorphisme de groupe
par une opération de
ce type (on dit que les transpositions sont toutes conjuguées).
Considérons maintenant un homomorphisme de groupe 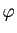 de
de
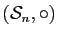 dans
dans
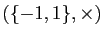 . Comme
. Comme 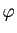 est
un homomorphisme de groupes,
est
un homomorphisme de groupes,
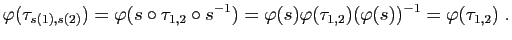
Toutes les transpositions, puisqu'elles sont conjuguées, doivent
avoir la même image par 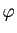 . Supposons que cette image commune soit
. Supposons que cette image commune soit
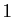 . Dans la mesure où toute permutation s'écrit commme un produit
de transpositions (proposition 2), on
obtient
. Dans la mesure où toute permutation s'écrit commme un produit
de transpositions (proposition 2), on
obtient 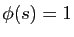 pour toute permutation
pour toute permutation
 . Dans ce cas, l'homomorphisme
. Dans ce cas, l'homomorphisme 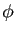 est constant et donc non surjectif.
Si
est constant et donc non surjectif.
Si 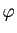 est supposé surjectif, alors
nécessairement l'image de toute transposition doit valoir
est supposé surjectif, alors
nécessairement l'image de toute transposition doit valoir  . Donc
. Donc
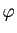 coïncide avec
coïncide avec
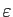 sur toutes les
transpositions. Mais puisque toute permutation est produit de
transpositions et que
sur toutes les
transpositions. Mais puisque toute permutation est produit de
transpositions et que 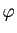 et
et
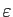 sont tous les deux
des homorphismes de groupes,
sont tous les deux
des homorphismes de groupes,

 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
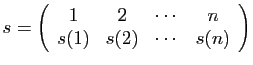
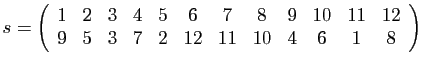

![]() une permutation quelconque : multiplions la transposition
une permutation quelconque : multiplions la transposition
![]() à droite par
à droite par ![]() et à gauche par
et à gauche par ![]() : on
obtient la transposition
: on
obtient la transposition
![]() . N'importe quelle
transposition se déduit donc de
. N'importe quelle
transposition se déduit donc de
![]() par une opération de
ce type (on dit que les transpositions sont toutes conjuguées).
Considérons maintenant un homomorphisme de groupe
par une opération de
ce type (on dit que les transpositions sont toutes conjuguées).
Considérons maintenant un homomorphisme de groupe ![]() de
de
![]() dans
dans
![]() . Comme
. Comme ![]() est
un homomorphisme de groupes,
est
un homomorphisme de groupes,
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales