La solidité des pyramides

L'interprétation d'un déterminant comme un volume est attribuée à Joseph-Louis Lagrange (1736-1813). Voici ce qu'il écrit dans «Nouvelle solution du problème du mouvement de rotation d'un corps de figure quelconque qui n'est animé par aucune force accélératrice», paru aux « Nouveaux mémoires de l'Académie Royale des Sciences et Belles-Lettres de Berlin», en 1773.

Imaginons maintenant une pyramide triangulaire qui ait ses quatre angles, l'un au centre des coordonnées, les autres aux points $M$, $M'$, $M''$, il n'est pas difficile de prouver que la solidité de cette pyramide sera exprimée par les coordonnées $x,y,z,x',y',z',\ldots$ de cette manière.

$$\frac{z(x'y''-y'x'')+z'(yx''-xy'')+z''(xy'-yx')}{6} \;,$$

[...]

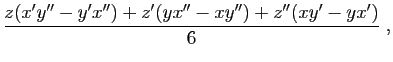
Ainsi cette quantité sera nulle toutes les fois que la pyramide en question s'évanouira, ce qui arrive lorsque les trois points $M$, $M'$, $M''$ sont dans un même plan passant par le centre des coordonnées.