Le logarithme népérien vous a sans doute
été présenté comme la primitive de la fonction
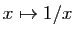 qui s'annule en
qui s'annule en 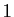 , et l'exponentielle comme sa fonction
réciproque. On en déduit alors les propriétés de ces deux
fonctions. Nous allons voir une autre définition.
, et l'exponentielle comme sa fonction
réciproque. On en déduit alors les propriétés de ces deux
fonctions. Nous allons voir une autre définition.
Le but de ce qui suit est de construire les fonctions exponentielle et
logarithme, et d'en démontrer les principales propriétés,
à partir de la propriété fondamentale de l'exponentielle,
qui est de transformer les sommes en produit.
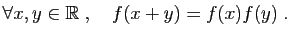 |
(3) |
Cette construction illustrera l'utilisation des outils de base de
l'analyse : limites, continuité, dérivabilité, convexité.
Dans un premier temps, nous raisonnerons par condition nécessaire,
en supposant l'existence d'une fonction  vérifiant
(3), pour en déduire ses propriétés.
vérifiant
(3), pour en déduire ses propriétés.
Démonstration : Si 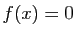 , alors pour tout
, alors pour tout
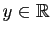 ,
,
Donc, soit  est identiquement nulle,
soit elle ne s'annule jamais. Comme
est identiquement nulle,
soit elle ne s'annule jamais. Comme
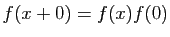 , si
, si
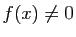 , alors
, alors
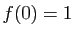 . Ensuite,
. Ensuite,
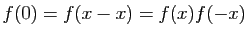 , d'où le point
2. Le point 3 se vérifie aussi facilement,
par récurrence sur
, d'où le point
2. Le point 3 se vérifie aussi facilement,
par récurrence sur 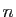 .
. 
Démonstration : D'après la proposition 10, si  est non nulle, alors
est non nulle, alors
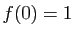 . Comme
. Comme  est continue en 0, il existe
est continue en 0, il existe 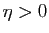 tel que
pour tout
tel que
pour tout
![$ x\in ]-\eta,\eta[ $](img615.gif) ,
, 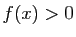 . Soit
. Soit
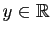 quelconque ; il
existe
quelconque ; il
existe
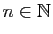 tel que
tel que
![$ y/n\in ]- \eta,\eta[ $](img617.gif) . D'après le point
3 de la proposition 10,
. D'après le point
3 de la proposition 10,
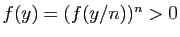 .
.
Montrons maintenant la continuité en un point 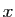 quelconque de
quelconque de
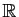 .
.
car  est continue en 0 et
est continue en 0 et 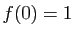 .
.
La démonstration de la convexité est plus difficile. Nous
souhaitons montrer que pour tout 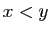 , et pour tout
, et pour tout
![$ \lambda\in[0,1]$](img239.gif) ,
,
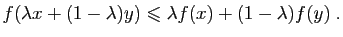 |
(4) |
Nous allons d'abord montrer que pour tout
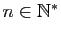 ,
,
 |
(5) |
D'après (3) et le point 3 de la proposition
10,
On pourrait en déduire (5), en utilisant...
la concavité du logarithme, que nous sommes précisément en train
de construire. Ce ne serait pas de jeu !
Nous allons démontrer (5) par récurrence sur 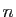 .
Observons d'abord que (5) est trivialement vraie pour
.
Observons d'abord que (5) est trivialement vraie pour
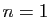 . Vérifions qu'elle est vraie pour
. Vérifions qu'elle est vraie pour 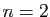 .
D'après (3) et puisque
.
D'après (3) et puisque  est strictement positive, on a :
est strictement positive, on a :
Il est facile de vérifier que si  et
et 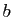 sont deux réels
positifs, alors
sont deux réels
positifs, alors
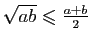 , d'où (5)
pour
, d'où (5)
pour 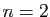 .
Nous en déduisons ensuite que si (5) est vraie pour un
entier
.
Nous en déduisons ensuite que si (5) est vraie pour un
entier 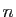 , alors elle est vraie pour
, alors elle est vraie pour 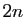 . En effet :
. En effet :
Montrons maintenant que si (5) est vraie pour un entier
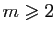 , alors elle est vraie pour
, alors elle est vraie pour 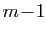 .
.
Soit en regroupant les termes :
d'où le résultat pour 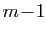 . Maintenant, si (5)
est vraie pour un entier
. Maintenant, si (5)
est vraie pour un entier 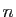 , elle est vraie pour
, elle est vraie pour 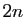 , et d'après
ce qui précède, aussi pour
, et d'après
ce qui précède, aussi pour 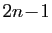 ,
, 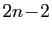 , ...,
, ...,
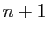 . Elle est donc vraie pour tout
. Elle est donc vraie pour tout 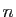 .
.
Soient 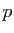 et
et 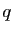 deux entiers positifs tels que
deux entiers positifs tels que 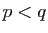 , et
, et 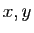 deux
réels tels que
deux
réels tels que 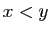 . Appliquons (5) pour
. Appliquons (5) pour 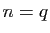 ,
,
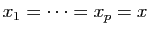 , et
, et
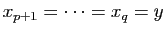 . On obtient :
. On obtient :
soit (4) pour
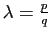 . Donc (4) est vraie
pour tout
. Donc (4) est vraie
pour tout 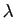 rationnel. Mais tout réel étant limite d'une
suite de rationnels, et la fonction
rationnel. Mais tout réel étant limite d'une
suite de rationnels, et la fonction  étant continue, (4)
est aussi vraie pour tout
étant continue, (4)
est aussi vraie pour tout 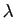 réel, donc
réel, donc  est convexe.
est convexe.
La dérivabilité se déduit de la convexité, en utilisant la
propriété (3). Commençons par montrer que  est
dérivable en 0. Considérons la fonction
est
dérivable en 0. Considérons la fonction 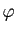 , qui à
, qui à
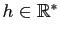 associe l'accroissement :
associe l'accroissement :
La fonction  étant convexe, ses accroissements sont croissants,
donc la fonction
étant convexe, ses accroissements sont croissants,
donc la fonction 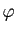 admet une limite à gauche et une limite
à droite en 0. La fonction
admet une limite à gauche et une limite
à droite en 0. La fonction  est donc dérivable à gauche et
à droite en 0. Nous devons montrer que les deux dérivées sont
égales. Pour cela, calculons
est donc dérivable à gauche et
à droite en 0. Nous devons montrer que les deux dérivées sont
égales. Pour cela, calculons
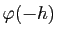 , en utilisant le point
2 de la proposition 10.
, en utilisant le point
2 de la proposition 10.
Or quand 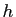 tend vers 0,
tend vers 0,
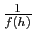 tend vers
tend vers 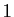 , par
continuité de
, par
continuité de  en 0. Donc la limite à gauche de
en 0. Donc la limite à gauche de 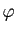 en
0 est égale à sa limite à droite, ce qui entraîne que
en
0 est égale à sa limite à droite, ce qui entraîne que  est dérivable en 0. Pour en déduire la dérivabilité en un
point
est dérivable en 0. Pour en déduire la dérivabilité en un
point 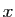 quelconque de
quelconque de
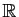 , il suffit d'appliquer une fois de plus
la propriété (3) :
, il suffit d'appliquer une fois de plus
la propriété (3) :
Puisque  est strictement positive,
est strictement positive,
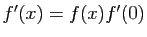 est de signe
constant. La fonction
est de signe
constant. La fonction  est :
est :
- strictement croissante si
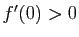 ,
,
- constante (et égale à
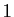 ) si
) si 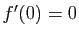 ,
,
- strictement décroissante si
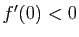 .
.
 Jusqu'ici nous n'avons raisonné que par condition nécessaire :
rien ne prouve encore qu'il existe des fonctions
Jusqu'ici nous n'avons raisonné que par condition nécessaire :
rien ne prouve encore qu'il existe des fonctions  vérifiant les
hypothèses des deux propositions précédentes.
vérifiant les
hypothèses des deux propositions précédentes.
Proposition 12
Pour tout 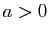 , il existe une unique fonction
, il existe une unique fonction  , continue en 0,
vérifiant
, continue en 0,
vérifiant (
3)
, et telle que 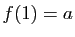 .
.
Démonstration : La fonction qui répond à la question est évidemment celle qui
à
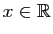 associe
associe
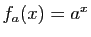 . Encore faut-il préciser sa
définition, et montrer qu'elle est la seule.
. Encore faut-il préciser sa
définition, et montrer qu'elle est la seule.
Si 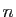 est un entier positif,
est un entier positif, 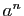 est le produit de
est le produit de 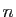 facteurs
égaux à
facteurs
égaux à  , et
, et
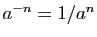 . La fonction qui à
. La fonction qui à  associe
associe 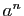 est strictement croissante et bijective de
est strictement croissante et bijective de
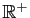 dans
dans
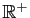 . Donc sa réciproque est aussi strictement croissante et
bijective de
. Donc sa réciproque est aussi strictement croissante et
bijective de
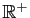 dans
dans
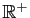 . Si
. Si  est un réel positif, le
réel
est un réel positif, le
réel 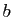 tel que
tel que 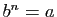 est donc défini de façon unique, et
on convient de le noter
est donc défini de façon unique, et
on convient de le noter
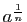 , de sorte que
, de sorte que
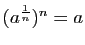 .
Si
.
Si
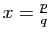 est un rationnel, nous savons donc définir
est un rationnel, nous savons donc définir
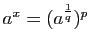 . Cette définition, et les
propriétés des puissances entières, entraînent que
la propriété (3) est vérifiée pour tout couple
. Cette définition, et les
propriétés des puissances entières, entraînent que
la propriété (3) est vérifiée pour tout couple
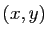 de rationnels :
de rationnels :
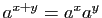 .
.
Nous souhaitons étendre la définition de 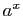 à tous les réels, par
continuité. Observons d'abord que nous pouvons, sans perte de
généralité, supposer que
à tous les réels, par
continuité. Observons d'abord que nous pouvons, sans perte de
généralité, supposer que 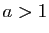 et
et 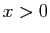 , grâce à la
propriété
, grâce à la
propriété
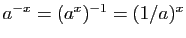 . Si
. Si 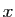 et
et 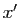 sont deux
rationnels tels que
sont deux
rationnels tels que 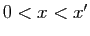 , alors
, alors
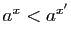 . Une des propriétés
fondamentales de l'ensemble
. Une des propriétés
fondamentales de l'ensemble
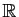 est que tout réel est la borne
supérieure de l'ensemble des rationnels qui lui sont inférieurs.
Si
est que tout réel est la borne
supérieure de l'ensemble des rationnels qui lui sont inférieurs.
Si 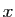 est un réel quelconque
et
est un réel quelconque
et 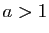 , nous pouvons donc définir
, nous pouvons donc définir 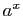 comme :
comme :
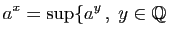
et
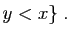
Il reste à vérifier que la fonction ainsi définie est bien
continue, et qu'on a donc aussi :
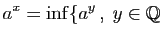
et
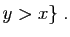
Pour cela, commençons par montrer que si 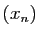 est
une suite de rationnels positifs, tendant vers 0, alors
est
une suite de rationnels positifs, tendant vers 0, alors 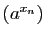 converge vers
converge vers 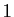 . Fixons
. Fixons
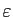 tel que
tel que
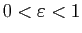 . Considérons les deux suites
. Considérons les deux suites
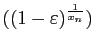 et
et
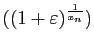 .
Si la suite
.
Si la suite 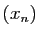 tend vers 0, la suite
tend vers 0, la suite
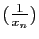 tend
vers
tend
vers 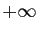 .
Si
.
Si 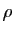 est un réel positif,
alors quand
est un réel positif,
alors quand
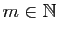 tend vers l'infini,
tend vers l'infini,
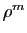 tend vers 0 si
tend vers 0 si 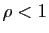 , vers
, vers 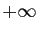 si
si 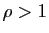 .
On en déduit que
.
On en déduit que
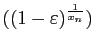 converge vers 0, alors que
converge vers 0, alors que
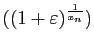 converge vers
converge vers 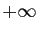 . Donc il
existe
. Donc il
existe 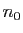 tel que pour tout
tel que pour tout 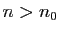 ,
,
soit
![$ a^{x_n}\in [1-\varepsilon,1+\varepsilon]$](img692.gif) .
Si les
.
Si les 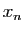 sont des rationnels négatifs, la conclusion est
la même car
sont des rationnels négatifs, la conclusion est
la même car
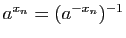 . Donc la conclusion reste
vraie pour une suite de rationnels
. Donc la conclusion reste
vraie pour une suite de rationnels 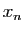 de signe quelconque.
On en déduit donc que la fonction que nous avons définie est bien
continue en 0.
de signe quelconque.
On en déduit donc que la fonction que nous avons définie est bien
continue en 0.
Pour 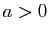 , la fonction qui à
, la fonction qui à 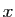 associe
associe 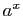 est donc continue en
0, elle est non nulle, et elle vérifie (3) pour tout
est donc continue en
0, elle est non nulle, et elle vérifie (3) pour tout
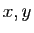 rationnels, donc pour tout
rationnels, donc pour tout 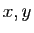 réels, en passant à la
limite. D'après le point 2 de la
proposition 11, elle est donc
continue sur
réels, en passant à la
limite. D'après le point 2 de la
proposition 11, elle est donc
continue sur
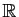 .
.
Pour l'unicité, il suffit d'observer que si une fonction  vérifie (3) et est telle que
vérifie (3) et est telle que 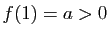 , alors par la
proposition 10, elle est telle que
, alors par la
proposition 10, elle est telle que 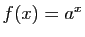 , pour tout
, pour tout
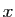 rationnel. Deux fonctions continues qui coïncident sur les
rationnels, sont nécessairement égales (tout
réel est limite d'une suite de rationnels). Donc
rationnel. Deux fonctions continues qui coïncident sur les
rationnels, sont nécessairement égales (tout
réel est limite d'une suite de rationnels). Donc 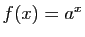 , pour
tout
, pour
tout 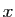 réel.
réel.  Pour
Pour 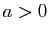 , notons
, notons 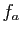 l'unique fonction continue en 0,
vérifiant (3), et telle que
l'unique fonction continue en 0,
vérifiant (3), et telle que 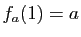 , à savoir
la fonction qui à
, à savoir
la fonction qui à
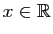 associe
associe 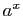 .
.
Puisque 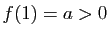 , la fonction
, la fonction  est non nulle et on peut lui appliquer
la proposition 11 :
est non nulle et on peut lui appliquer
la proposition 11 : 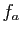 est
dérivable sur
est
dérivable sur
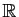 .
.
Définition 8
On appelle logarithme, et on note 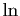 la fonction définie sur
la fonction définie sur
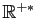 , qui à
, qui à 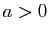 associe
associe
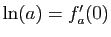 .
.
Proposition 13
- Pour tout
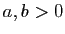 , on a :
, on a :
- Pour tout
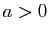 et
et
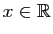 , on a :
, on a :
- La fonction
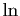 est strictement croissante, et :
est strictement croissante, et :
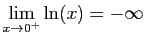
et
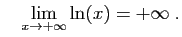
Démonstration : Pour le premier point, soient  et
et 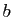 deux réels strictement
positifs, et considérons la fonction
deux réels strictement
positifs, et considérons la fonction 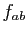 . On a :
. On a :
On calcule donc la dérivée de 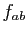 en 0, en dérivant le
produit
en 0, en dérivant le
produit 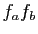 :
:
Pour le point 2, soit 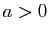 et
et 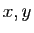 deux réels.
deux réels.
Fixons 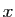 , dérivons par rapport à
, dérivons par rapport à 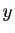 et prenons la dérivée en
0.
On obtient :
et prenons la dérivée en
0.
On obtient :
d'où le résultat.
Passons au point 3. Fixons 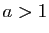 . La fonction
. La fonction 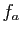 est alors
strictement croissante, elle admet donc une limite en
est alors
strictement croissante, elle admet donc une limite en 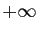 . Or la
suite
. Or la
suite 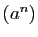 tend vers
tend vers 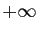 , donc la limite de
, donc la limite de 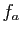 en
en
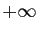 est
est 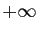 . La relation
. La relation
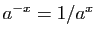 montre que la
limite de
montre que la
limite de 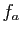 en
en 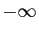 est 0. La fonction
est 0. La fonction 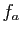 est donc
bijective, de
est donc
bijective, de
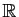 dans
dans
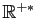 . La relation
. La relation
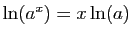 montre que la fonction réciproque de
montre que la fonction réciproque de 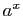 est la fonction qui à
est la fonction qui à
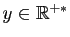 associe
associe
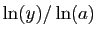 . Cette fonction est donc
strictement croissante et bijective de
. Cette fonction est donc
strictement croissante et bijective de
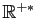 dans
dans
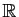 .
.  Il nous reste à définir la fonction exponentielle, qui est la
réciproque du logarithme. D'après le point 3 de la
proposition 13, il existe un réel unique, strictement
positif, dont le logarithme vaut
Il nous reste à définir la fonction exponentielle, qui est la
réciproque du logarithme. D'après le point 3 de la
proposition 13, il existe un réel unique, strictement
positif, dont le logarithme vaut 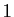 . On le note
. On le note
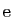 .
.
Définition 9
On appelle exponentielle, et on note 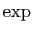 , la fonction qui à
, la fonction qui à
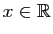 associe
associe
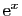 , où
, où
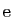 est l'unique réel
tel que
est l'unique réel
tel que
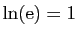 .
.
Proposition 14
L'exponentielle est la réciproque du logarithme. Les deux fonctions
sont strictement croissantes et dérivables.
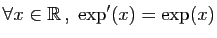
et
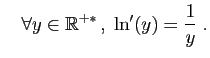
Puisque 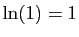 , on a
, on a
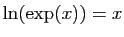 , par le point 2 de la
proposition 13. La dérivée de l'exponentielle est
donnée par le point 4 de la proposition 11. On
dérive le logarithme comme une fonction réciproque :
, par le point 2 de la
proposition 13. La dérivée de l'exponentielle est
donnée par le point 4 de la proposition 11. On
dérive le logarithme comme une fonction réciproque :
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
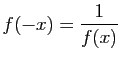
![]() quelconque de
quelconque de
![]() .
.
![]() , et pour tout
, et pour tout
![]() ,
,
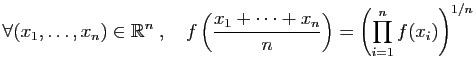
![]() .
Observons d'abord que (5) est trivialement vraie pour
.
Observons d'abord que (5) est trivialement vraie pour
![]() . Vérifions qu'elle est vraie pour
. Vérifions qu'elle est vraie pour ![]() .
D'après (3) et puisque
.
D'après (3) et puisque ![]() est strictement positive, on a :
est strictement positive, on a :
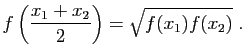
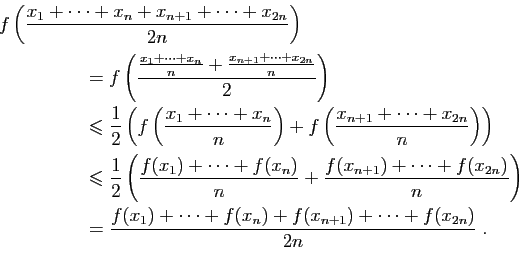
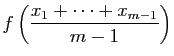
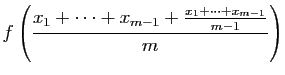
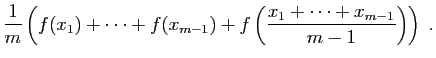
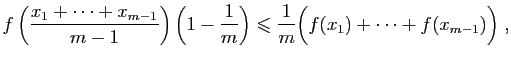
![]() et
et ![]() deux entiers positifs tels que
deux entiers positifs tels que ![]() , et
, et ![]() deux
réels tels que
deux
réels tels que ![]() . Appliquons (5) pour
. Appliquons (5) pour ![]() ,
,
![]() , et
, et
![]() . On obtient :
. On obtient :
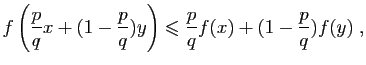
![]() est
dérivable en 0. Considérons la fonction
est
dérivable en 0. Considérons la fonction ![]() , qui à
, qui à
![]() associe l'accroissement :
associe l'accroissement :
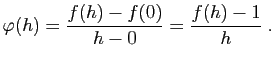
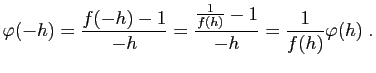
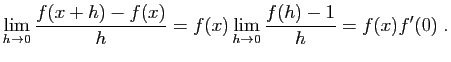
![]() est un entier positif,
est un entier positif, ![]() est le produit de
est le produit de ![]() facteurs
égaux à
facteurs
égaux à ![]() , et
, et
![]() . La fonction qui à
. La fonction qui à ![]() associe
associe ![]() est strictement croissante et bijective de
est strictement croissante et bijective de
![]() dans
dans
![]() . Donc sa réciproque est aussi strictement croissante et
bijective de
. Donc sa réciproque est aussi strictement croissante et
bijective de
![]() dans
dans
![]() . Si
. Si ![]() est un réel positif, le
réel
est un réel positif, le
réel ![]() tel que
tel que ![]() est donc défini de façon unique, et
on convient de le noter
est donc défini de façon unique, et
on convient de le noter
![]() , de sorte que
, de sorte que
![]() .
Si
.
Si
![]() est un rationnel, nous savons donc définir
est un rationnel, nous savons donc définir
![]() . Cette définition, et les
propriétés des puissances entières, entraînent que
la propriété (3) est vérifiée pour tout couple
. Cette définition, et les
propriétés des puissances entières, entraînent que
la propriété (3) est vérifiée pour tout couple
![]() de rationnels :
de rationnels :
![]() .
.
![]() à tous les réels, par
continuité. Observons d'abord que nous pouvons, sans perte de
généralité, supposer que
à tous les réels, par
continuité. Observons d'abord que nous pouvons, sans perte de
généralité, supposer que ![]() et
et ![]() , grâce à la
propriété
, grâce à la
propriété
![]() . Si
. Si ![]() et
et ![]() sont deux
rationnels tels que
sont deux
rationnels tels que ![]() , alors
, alors
![]() . Une des propriétés
fondamentales de l'ensemble
. Une des propriétés
fondamentales de l'ensemble
![]() est que tout réel est la borne
supérieure de l'ensemble des rationnels qui lui sont inférieurs.
Si
est que tout réel est la borne
supérieure de l'ensemble des rationnels qui lui sont inférieurs.
Si ![]() est un réel quelconque
et
est un réel quelconque
et ![]() , nous pouvons donc définir
, nous pouvons donc définir ![]() comme :
comme :
![]() , la fonction qui à
, la fonction qui à ![]() associe
associe ![]() est donc continue en
0, elle est non nulle, et elle vérifie (3) pour tout
est donc continue en
0, elle est non nulle, et elle vérifie (3) pour tout
![]() rationnels, donc pour tout
rationnels, donc pour tout ![]() réels, en passant à la
limite. D'après le point 2 de la
proposition 11, elle est donc
continue sur
réels, en passant à la
limite. D'après le point 2 de la
proposition 11, elle est donc
continue sur
![]() .
.
![]() vérifie (3) et est telle que
vérifie (3) et est telle que ![]() , alors par la
proposition 10, elle est telle que
, alors par la
proposition 10, elle est telle que ![]() , pour tout
, pour tout
![]() rationnel. Deux fonctions continues qui coïncident sur les
rationnels, sont nécessairement égales (tout
réel est limite d'une suite de rationnels). Donc
rationnel. Deux fonctions continues qui coïncident sur les
rationnels, sont nécessairement égales (tout
réel est limite d'une suite de rationnels). Donc ![]() , pour
tout
, pour
tout ![]() réel.
réel. ![]() Pour
Pour ![]() , notons
, notons ![]() l'unique fonction continue en 0,
vérifiant (3), et telle que
l'unique fonction continue en 0,
vérifiant (3), et telle que ![]() , à savoir
la fonction qui à
, à savoir
la fonction qui à
![]() associe
associe ![]() .
.
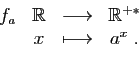
![]() . La fonction
. La fonction ![]() est alors
strictement croissante, elle admet donc une limite en
est alors
strictement croissante, elle admet donc une limite en ![]() . Or la
suite
. Or la
suite ![]() tend vers
tend vers ![]() , donc la limite de
, donc la limite de ![]() en
en
![]() est
est ![]() . La relation
. La relation
![]() montre que la
limite de
montre que la
limite de ![]() en
en ![]() est 0. La fonction
est 0. La fonction ![]() est donc
bijective, de
est donc
bijective, de
![]() dans
dans
![]() . La relation
. La relation
![]() montre que la fonction réciproque de
montre que la fonction réciproque de ![]() est la fonction qui à
est la fonction qui à
![]() associe
associe
![]() . Cette fonction est donc
strictement croissante et bijective de
. Cette fonction est donc
strictement croissante et bijective de
![]() dans
dans
![]() .
. ![]() Il nous reste à définir la fonction exponentielle, qui est la
réciproque du logarithme. D'après le point 3 de la
proposition 13, il existe un réel unique, strictement
positif, dont le logarithme vaut
Il nous reste à définir la fonction exponentielle, qui est la
réciproque du logarithme. D'après le point 3 de la
proposition 13, il existe un réel unique, strictement
positif, dont le logarithme vaut ![]() . On le note
. On le note
![]() .
.
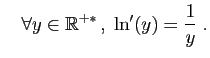
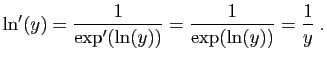
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales