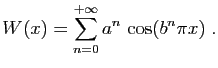
Jusqu'au XIXe siècle, tout le monde pensait que toute courbe continue devait admettre des tangentes, sauf peut-être en quelques points isolés, comme la fonction valeur absolue. Dans un mémoire de 1806, Ampère avait même tenté de le démontrer. Aussi beaucoup furent-ils choqués quand Weierstrass donna un exemple de fonction continue, mais dérivable en aucun point. La fonction de Weierstrass s'exprime sous forme de série trigonométrique.
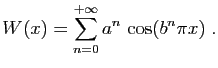
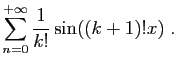
L'agitation désordonnée de particules dans un fluide avait été observée par le biologiste anglais Brown au début du XIXe siècle, mais il fallut assez longtemps pour que les physiciens établissent le rapport entre le mouvement des particules et la diffusion de la chaleur. Dans un de ses articles de 1905, Albert Einstein proposa une modélisation cinétique de ce mouvement, dont découlait l'équation de la chaleur, établie par Fourier en 1808. Le travail, poursuivi par Perrin en 1909, conduisit à une étude théorique du mouvement brownien, comme objet mathématique, par Wiener en 1923. Dès ses premiers mots sur le mouvement brownien, Wiener cite un article de Perrin, qui évoque les courbes sans tangente des mathématiciens. Et de fait, Wiener bâtit un modèle dans lequel les trajectoires sont continues, avec une vitesse infinie en tout point.
Quel est ce modèle ? Pour s'en faire une idée, le plus
simple est de partir du jeu de pile ou face. Si la
pièce est équilibrée, le joueur a une chance sur deux de gagner
un euro, et une chance sur deux de perdre un euro. Le gain ou la perte
au fil des parties est la somme cumulée des gains ou pertes de
chaque partie. Partant d'une fortune nulle, la fortune ![]() du
joueur à la
du
joueur à la ![]() -ième partie est aléatoire.
La figure 10 représente 3
trajectoires de
-ième partie est aléatoire.
La figure 10 représente 3
trajectoires de ![]() en fonction de
en fonction de ![]() ,
sur
,
sur ![]() parties jouées. Ces courbes donnent une bonne idée de
ce que sont les trajectoires du mouvement brownien. Pour le définir,
on accélère l'échelle de temps d'un
facteur
parties jouées. Ces courbes donnent une bonne idée de
ce que sont les trajectoires du mouvement brownien. Pour le définir,
on accélère l'échelle de temps d'un
facteur ![]() , et on raccourcit l'échelle des fortunes d'un
facteur
, et on raccourcit l'échelle des fortunes d'un
facteur ![]() . On peut définir le mouvement brownien
à l'instant
. On peut définir le mouvement brownien
à l'instant ![]() comme la limite suivante.
comme la limite suivante.
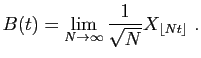
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales