Le verset 12 des «Harmonies Célestes»1, écrit en 499 par Aryabhata est
une collection de 24 nombres :
Il faut comprendre ces nombres comme les différences successives entre les demi-cordes des angles
obtenus en divisant en 24 parties égales un quart de cercle de rayon 3428 (la somme des 24 valeurs). En clair :
les 24 sommes cumulées, divisées par 3428 sont des valeurs
approchées de
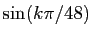 , pour
, pour 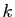 allant de
1 à 24. Faites le calcul : la différence maximale en valeur
absolue entre les valeurs d'Aryabhata
et les valeurs exactes est de
allant de
1 à 24. Faites le calcul : la différence maximale en valeur
absolue entre les valeurs d'Aryabhata
et les valeurs exactes est de
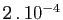 : pas si mal pour
quelqu'un qui ne travaillait qu'avec des entiers !
Un peu plus loin, Aryabhata montre qu'il avait finement observé
la décroissance de ses tables
de différences : «Les différences sont diminuées des
quotients successifs des sinus par le premier sinus».
En clair, si
: pas si mal pour
quelqu'un qui ne travaillait qu'avec des entiers !
Un peu plus loin, Aryabhata montre qu'il avait finement observé
la décroissance de ses tables
de différences : «Les différences sont diminuées des
quotients successifs des sinus par le premier sinus».
En clair, si 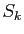 désigne la
désigne la 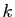 -ième valeur cumulée :
-ième valeur cumulée :
Ramené aux différences de sinus successifs, Aryabhata n'est
pas loin d'exprimer un double taux d'accroissement :
Mais parler de dérivée seconde au temps d'Aryabhata serait
anachronique, d'autant plus que sa règle ne s'appliquait
qu'aux multiples de 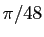 . Le premier astronome indien à formuler
une règle de calcul approchée générale pour de petites
différences de sinus est Manjula (932) :
. Le premier astronome indien à formuler
une règle de calcul approchée générale pour de petites
différences de sinus est Manjula (932) :
Cette règle empirique sera reprise par Aryabhata II (950) et
Bhaskara II (1150). Ce dernier donne une justification
géométrique de la formule, et est parfaitement conscient qu'elle
est d'autant meilleure que 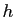 est petit : il parle à cette
occasion d'«immesurablement petit». Il exprime même les
notions de «différence instantanée de sinus»
et «mouvement instantané». Cela suffit-il pour en faire
l'inventeur des dérivées ?
Peut-être pas car il ne dit jamais explicitement que le cosinus
est la dérivée du sinus. Pourtant il est conscient du fait que
quand une fonction atteint son maximum, sa
«différence instantanée» s'annule. Il observe aussi que
quand une planète est à son apogée ou à son
périgée, la différence entre sa position observée et sa
position prédite pour un mouvement uniforme s'annule
et il en déduit qu'en un certain point intermédiaire
l'incrément de cette quantité
doit aussi s'annuler : c'est le théorème de Rolle !
est petit : il parle à cette
occasion d'«immesurablement petit». Il exprime même les
notions de «différence instantanée de sinus»
et «mouvement instantané». Cela suffit-il pour en faire
l'inventeur des dérivées ?
Peut-être pas car il ne dit jamais explicitement que le cosinus
est la dérivée du sinus. Pourtant il est conscient du fait que
quand une fonction atteint son maximum, sa
«différence instantanée» s'annule. Il observe aussi que
quand une planète est à son apogée ou à son
périgée, la différence entre sa position observée et sa
position prédite pour un mouvement uniforme s'annule
et il en déduit qu'en un certain point intermédiaire
l'incrément de cette quantité
doit aussi s'annuler : c'est le théorème de Rolle !
Du XIVe au XVIe siècle, à la suite
de Madhava (1340-1425) une importante école d'astronomie fleurit
dans
l'état du Kérala, au Sud de l'Inde. Fidèles à la tradition de
leurs ancêtres, ces astronomes
développent encore le calcul différentiel. Ainsi le théorème
des valeurs intermédiaires sera énoncé explicitement au
XVe siècle
par Parameshvara (1370-1460) dans «Lilavati Bhasya» qui est un
commentaire du Lilavati de Bhaskara.
Certains ont accusé Newton et Leibniz d'avoir, deux siècles plus tard,
pillé les résultats des mathématiciens du Kérala. C'est
oublier un peu vite que, malgré des algorithmes d'approximations
impressionnants, ceux-ci n'ont jamais défini les notions de
dérivée et d'intégrale, ni surtout établi leur
réciprocité.
Il n'existe aucune preuve que les résultats de l'école du Kérala
aient été connus en dehors de l'Inde avant le XIXe siècle.
Mais peut-être serez-vous tentés de répondre à la question «
qui de Newton ou Leibniz
a inventé le calcul infinitésimal ?»
par : ni l'un ni l'autre !
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
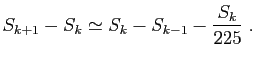
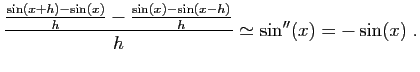
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales