Newton et Leibniz

Les problèmes de quadrature (intégration) et de tangente (dérivation) ont passionné de nombreux mathématiciens depuis Archimède. Les premiers à avoir compris le rapport entre les deux sont Isaac Newton (1643-1727) et Gottfried Wilhem von Leibniz (1646-1716). Ils sont maintenant considérés comme co-inventeurs du calcul différentiel.

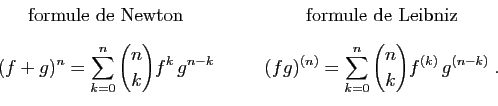
Pourtant la controverse a longtemps fait rage, du vivant de Newton et Leibniz, et pendant encore de nombreuses années après leur mort. Les uns, à la suite de Newton lui-même, accusaient Leibniz de plagiat, car il aurait eu accès à des manuscrits non publiés de Newton. Les autres prouvaient sans conteste l'antériorité des publications de Leibniz et la supériorité de son système de notation. Il semble bien que Newton avait effectivement développé ses idées avant Leibniz, mais que, même si ce dernier a eu accès à des manuscrits de Newton, il a travaillé de façon indépendante. La controverse, qui paraît de nos jours plutôt futile, eut pour conséquence de couper pendant longtemps les mathématiciens anglais du reste de l'Europe : ce n'est qu'au début du XIX^e siècle que les notations de Leibniz furent acceptées en Angleterre. Voici comment, dans Philosophiae Naturalis Principia Mathematica (1687), Newton exprime sa vision des dérivées.

Les rapports ultimes dans lesquels les quantités disparaissent ne sont pas réellement des rapports de quantités ultimes, mais les limites vers lesquelles les rapports de quantités, décroissant sans limite, s'approchent toujours, et vers lesquelles ils peuvent s'approcher aussi près qu'on veut.

La vision de Newton est très proche de notre définition moderne de la dérivée comme limite d'un taux d'accroissement. C'est d'autant plus remarquable que la notion de limite ne sera définie rigoureusement, que presque deux siècles après les premières découvertes de Newton. L'intuition de Newton est puissante, mais lui-même sent bien qu'il n'a pas défini ses quantités infinitésimales de manière suffisamment rigoureuse. D'ailleurs elles resteront longtemps pour beaucoup un «fantôme de quantités disparues». Peut-être est-ce une des raisons pour lesquelles Newton, dont les premiers travaux sur le sujet datent de 1664, n'achèvera son ouvrage «la méthode des fluxions et des suites infinies»  qu'en 1671, et ne le publiera pas de son vivant...  contrairement à Leibniz. Par un clin d'il de l'histoire, les noms de Newton et Leibniz sont restés attachés à deux formules extrêmement proches.

$$\begin{array}{ccc} \mbox{formule de Newton}&\quad&\mbox{form... ...} = \sum_{k=0}^n \binom{n}{k}f^{(k)} g^{(n-k)}}\;. \end{array}$$