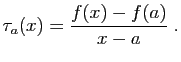
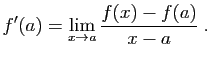
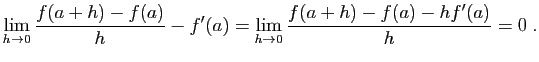
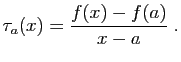
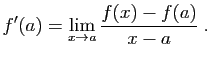
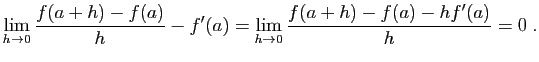
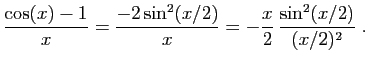
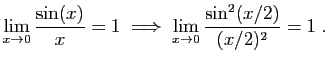
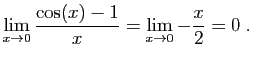
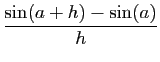 |
|||
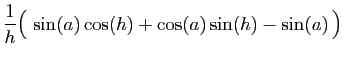 |
|||
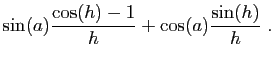 |
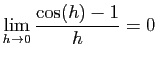 et
et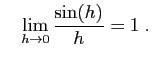
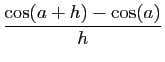 |
|||
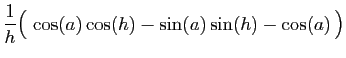 |
|||
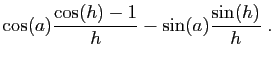 |
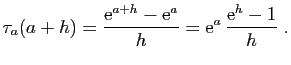
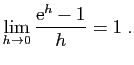
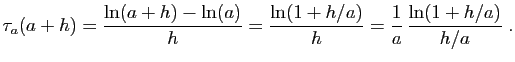
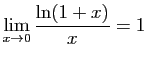 donc
donc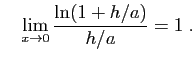
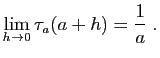
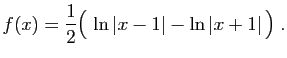
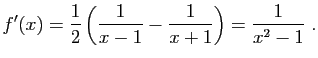
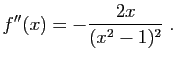
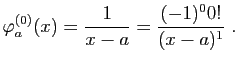
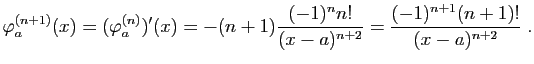
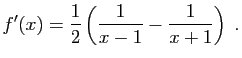
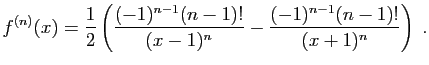
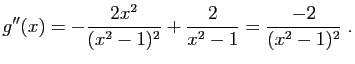
On montre de la même façon que ![]() est négative sur
est négative sur ![]() et
sur
et
sur
![]() (ou bien en remarquant que pour tout
(ou bien en remarquant que pour tout
![]() ,
,
![]() ). Donc :
). Donc :
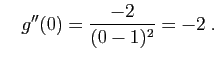
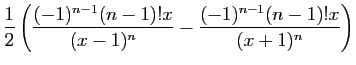 |
|||
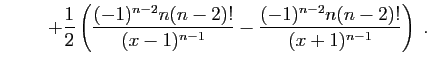 |
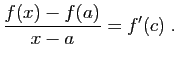
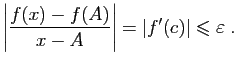
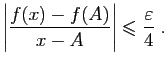
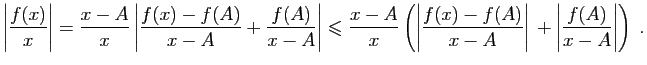
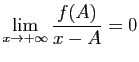 et
et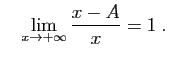
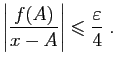
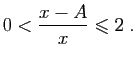
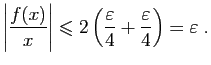
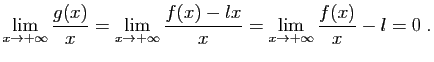
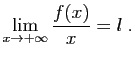
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales