Tout le monde peut se tromper

Avec une fausse modestie teintée de mauvaise foi, d'Alembert, deux ans avant sa mort écrit à Lagrange² :

Je m'amuse à repasser toutes les sottises mathématiques que j'ai écrites depuis quarante ans et je jette sur le papier quelques remarques que cette lecture me suggère ; mais ces remarques ne paraîtront tout au plus qu'après ma mort, si même ceux à qui je les laisserai les jugent dignes de paraître, ce qui est au moins fort douteux.

Des «sottises mathématiques» les plus grands en ont écrit, même Cauchy ! Pensez donc : 789 articles ! 27 épais volumes ! Fouiller les uvres complètes de Cauchy pour y détecter des incorrections ponctuelles est passablement vain, mais relativement facile. Celle qui suit est la plus célèbre ; elle se trouve dans le «Cours d'Analyse de l'École Royale Polytechnique, par M. Augustin-Louis Cauchy, Ingénieur des Ponts et Chaussées, Professeur d'Analyse à l'École Polytechnique, Membre de l'Académie des sciences, Chevalier de la Légion d'honneur».

Lorsque, les termes de la série (1) renfermant une même variable $x$, cette série est convergente, et ses différents termes fonctions continues de $x$, dans le voisinage d'une valeur particulière attribué à cette variable,

$$s_n\;,\quad r_n$$   et$$\quad s$$

sont encore trois fonctions de la variable $x$, dont la première est évidemment continue par rapport à $x$ dans le voisinage de la valeur particulière dont il s'agit. Cela posé, considérons les accroissements que reçoivent ces trois fonctions, lorsqu'on fait croître $x$ d'une quantité infiniment petite $\alpha$. L'accroissement de $s_n$ sera, pour toutes les valeurs possibles de $n$, une quantité infiniment petite ; et celui de $r_n$ deviendra insensible en même temps que $r_n$, si on attribue à $n$ une valeur très considérable. Par suite, l'accroissement de la fonction $s$ ne pourra être qu'une quantité infiniment petite. De cette remarque on déduit immédiatement la proposition suivante.

THÉORÈME I. - Lorque les différents termes de la série (1) sont des fonctions d'une même variable $x$, continues par rapport à cette variable dans le voisinage d'une valeur particulière pour laquelle la série est convergente, la somme de la série est aussi, dans le voisinage de cette valeur particulière, fonction continue de $x$.

En 1826, Abel est à Paris, où il espére faire (re)connaître ses travaux sur la résolution des équations du cinquième degré, ainsi que sur les fonctions elliptiques ³. Il a alors 24 ans, et ses contacts avec les plus grands mathématiciens du moment lui laissent une impression mitigée, qu'il exprime sans détour dans une lettre à son professeur norvégien.

Certes j'aurais dû t'écrire depuis longtemps, mais j'attendais d'abord la solution au sujet de mon mémoire que j'ai déposé à l'Institut. Mais ces hommes lents n'en finissent pas. Legendre et Cauchy étaient juges. Legendre est d'une complaisance extrême, mais malheureusement fort vieux. Cauchy est fou, et il est impossible d'avoir affaire avec lui. Pourtant c'est lui qui, à présent, est le mathématicien qui sait comment doivent être traitées les mathématiques. Ses travaux sont excellents ; mais il écrit obscurément. D'abord je ne comprenais rien à ses uvres ; maintenant j'y arrive mieux. [...] Cauchy est infiniment catholique et bigot. Chose bien singulière pour un mathématicien ! D'ailleurs, il est le seul qui travaille les mathématiques pures. Poisson, Fourier, Ampère, etc. s'occupent exclusivement de magnétisme et d'autres parties de la physique.

Quand il écrit pour publication, le ton est plus révérencieux.

Nous allons d'abord établir quelques théorèmes nécessaires sur les séries. L'excellent ouvrage de M. Cauchy «Cours d'analyse de l'école polytechnique», qui doit être lu par tout analyste qui aime la rigueur dans les recherches mathématiques, nous servira de guide.

Suivent quelques résultats, dont celui-ci.

Théorème V. Soit

$$v_0+v_1\delta+v_2\delta^2+\ldots$$ etc.

une série convergente, dans laquelle $v_0, v_1, v_2\ldots$ sont des fonctions continues d'une même quantité variable $x$ entre les limites $x=a$ et $x=b$, la série

$$f(x)=v_0+v_1\alpha+v_2\alpha^2+\ldots$$

où $\alpha<\delta$ sera convergente et fonction continue de $x$ entre les mêmes limites.

Et Abel d'ajouter une note de bas de page à la fin de la démonstration :

Dans l'ouvrage cité de M. Cauchy on trouve (p. 131) le théorème suivant : «Lorsque les différens termes de la série $u_0+u_1+u_2+\ldots$ etc. sont des fonctions d'une même variable $x$, continues par rapport à cette variable dans le voisinage d'une valeur particulière pour laquelle la série est convergente, la somme de la série est aussi, dans le voisinage de cette valeur particulière, fonction continue de $x$.» Mais il semble que ce théorème admet des exceptions. Par exemple la série

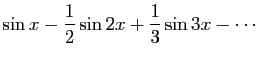$$\sin x -\frac{1}{2}\sin 2x +\frac{1}{3}\sin 3 x-\cdots$$ etc.

est discontinue pour toute valeur $(2m+1)\pi$ de $x$, où $m$ est un nombre entier. Il y a, comme on sait, plusieurs séries de cette espèce.

Des exceptions pour un théorème «démontré» ? Qu'en termes galants ces choses-là sont dites ! Et Cauchy, qu'en avait-il pensé ? Il était bel et bien responsable de la perte du mémoire d'Abel, qu'il ne retrouvera qu'après la mort prématurée de son auteur. Y aurait-il un lien avec le fait qu'Abel l'ait pris en défaut ? Impossible de le savoir. Il ne reviendra sur le sujet qu'en 1853 (sans citer Abel), dans une «Note sur les séries convergentes dont les divers termes sont des fonctions continues d'une variable réelle ou imaginaire, entre des limites données».

En établissant, dans mon «Analyse algébrique», les règles générales relatives à la convergence des séries, j'ai, de plus, énoncé le théorème suivant :

[...]

Comme l'ont remarqué MM. Bouquet et Briot, ce théorème se vérifie pour les séries ordonnées suivant les puissances ascendantes d'une variable. Mais pour d'autres séries, il ne saurait être admis sans restriction.

[...]

Au reste, il est facile de voir comment on doit modifier l'énoncé du théorème pour qu'il n'y ait plus lieu à aucune exception. C'est ce que je vais expliquer en peu de mots.

Ce «peu de mots» donne surtout l'impression que Cauchy remplace, sans dégager la notion d'uniformité, l'hypothèse de convergence par son critère, ce qui ne change pas grand chose au fait que le «théorème admet des exceptions».