 Toute courbe paramétrée de classe
Toute courbe paramétrée de classe 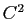 est régulière.
est régulière.
-
 Toute courbe paramétrée régulière a un espace tangent en tout point.
Toute courbe paramétrée régulière a un espace tangent en tout point.
 Si une courbe paramétrée admet une droite tangente en un point, alors elle est régulière en ce point.
Si une courbe paramétrée admet une droite tangente en un point, alors elle est régulière en ce point.
 Toute paramétrisation de la courbe géométrique d'équation
Toute paramétrisation de la courbe géométrique d'équation 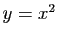 est régulière.
est régulière.
-
 Il existe une paramétrisation régulière de la courbe géométrique d'équation
Il existe une paramétrisation régulière de la courbe géométrique d'équation 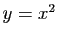 .
.
 Toute paramétrisation de la courbe géométrique d'équation
Toute paramétrisation de la courbe géométrique d'équation
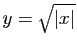 (avec
(avec
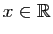 ) est régulière.
) est régulière.
 Il existe une paramétrisation régulière de la courbe géométrique d'équation
Il existe une paramétrisation régulière de la courbe géométrique d'équation
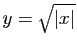 (avec
(avec
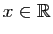 ).
).
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales