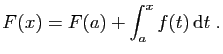
Puisque ![]() est continue, d'après le théorème des valeurs
intermédiaires, si
est continue, d'après le théorème des valeurs
intermédiaires, si ![]() ne s'annule pas sur
ne s'annule pas sur ![]() , alors son signe
reste le même :
, alors son signe
reste le même :
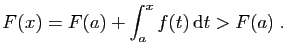
![$\displaystyle \int_a^x tf(t) \mathrm{d}t
= \Big[ tF(t)\Big]_a^x-\int_a^x F(t) \mathrm{d}t
=xF(x)-aF(a)-\int_a^x F(t) \mathrm{d}t\;.
$](img630.gif)
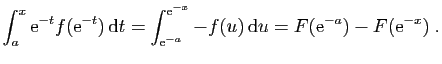
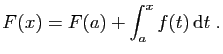
Puisque ![]() est continue, d'après le théorème des valeurs
intermédiaires, si
est continue, d'après le théorème des valeurs
intermédiaires, si ![]() ne s'annule pas sur
ne s'annule pas sur ![]() , alors son signe
reste le même :
, alors son signe
reste le même :
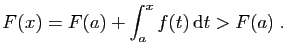
![$\displaystyle \int_a^x tf(t) \mathrm{d}t
= \Big[ tF(t)\Big]_a^x-\int_a^x F(t) \mathrm{d}t
=xF(x)-aF(a)-\int_a^x F(t) \mathrm{d}t\;.
$](img630.gif)
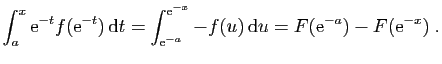
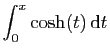 |
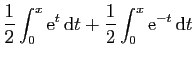 |
||
![$\displaystyle \displaystyle{\frac{1}{2}\Big[\mathrm{e}^t\Big]_0^x
+\frac{1}{2}\Big[-\mathrm{e}^{-t}\Big]_0^x}$](img634.gif) |
|||
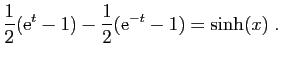 |
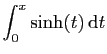 |
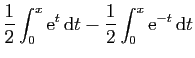 |
||
![$\displaystyle \displaystyle{\frac{1}{2}\Big[\mathrm{e}^t\Big]_0^x
-\frac{1}{2}\Big[-\mathrm{e}^{-t}\Big]_0^x}$](img638.gif) |
|||
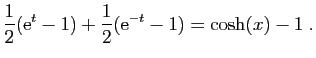 |
 |
|||
 |
|||
 |
|||
 |
|||
 |
|||
 |
|||
 |
|||
 |
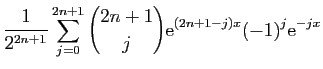 |
|||
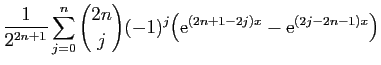 |
|||
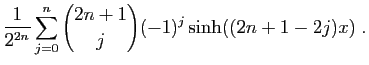 |
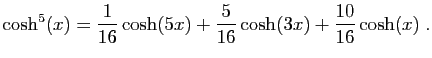
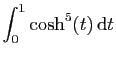 |
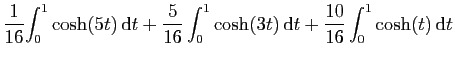 |
||
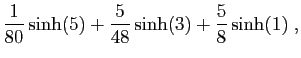 |
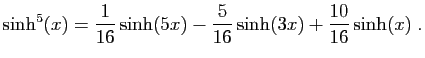
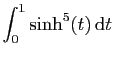 |
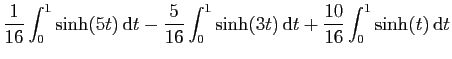 |
||
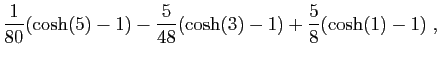 |
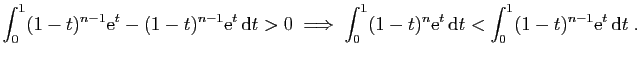
La fonction
![]() est majorée par
est majorée par
![]() sur
sur ![]() . De
plus la fonction
. De
plus la fonction
![]() est continue et
strictement positive sur
est continue et
strictement positive sur ![]() . Le
même raisonnement que précédemment donne la majoration
au sens strict suivante.
. Le
même raisonnement que précédemment donne la majoration
au sens strict suivante.
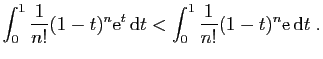
![$\displaystyle \int_0^1 (1-t)^{n} \mathrm{d}t=\left[ -\frac{1}{n+1}(1-t)^{n+1}\right]_0^1
=\frac{1}{n+1}\;.
$](img675.gif)
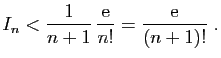
![$\displaystyle I_0=\int_0^1 \mathrm{e}^t \mathrm{d}t
=\Big[ \mathrm{e}^t\Big]_0^1=\mathrm{e}-1\;.
$](img677.gif)
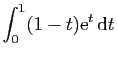 |
|||
![$\displaystyle \displaystyle{\Big[(1-t)\mathrm{e}^t\Big]_0^1+\int_0^1\mathrm{e}^t \mathrm{d}t}$](img680.gif) |
|||
![$\displaystyle \displaystyle{\left[\frac{1}{n!}(1-t)^n\mathrm{e}^t\right]_0^1
+\int_0^1 \frac{n}{n!}(1-t)^{n-1}\mathrm{e}^t \mathrm{d}t}$](img683.gif) |
|||
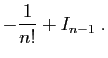 |
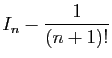 |
|||
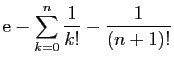 |
|||
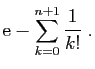 |
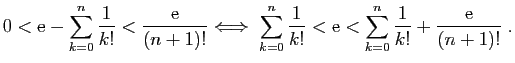
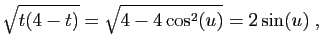
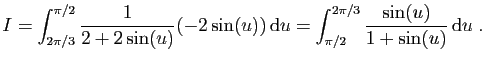
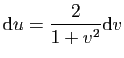 et
et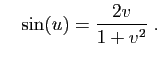

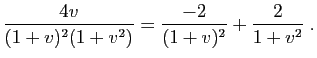
![$\displaystyle I = \left[\frac{2}{1+v}\right]_1^{\sqrt{3}}+
2\Big[\arctan(v)\Big...
...rac{2}{1+\sqrt{3}}-1+\frac{2\pi}{3}-
\frac{\pi}{2}=\frac{\pi}{6}-2+\sqrt{3}\;.
$](img715.gif)
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales