-
- Il existe des primitives de
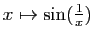 définies sur l'intervalle
définies sur l'intervalle ![$ [-1,1]$](img423.gif) .
.
-
- Il existe des primitives de
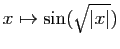 définies sur l'intervalle
définies sur l'intervalle ![$ [-1,1]$](img423.gif) .
.
-
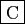
- Il existe des primitives de
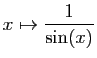 définies sur l'intervalle
définies sur l'intervalle ![$ [-1,1]$](img423.gif) .
.
-
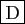
- L'intégrale de
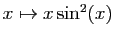 sur
sur
![$ [-\pi,\pi]$](img514.gif) est nulle.
est nulle.
-
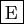
- L'intégrale de
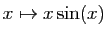 sur
sur
![$ [-\pi,\pi]$](img514.gif) est nulle.
est nulle.
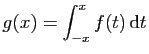
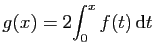
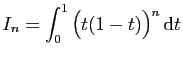
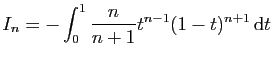
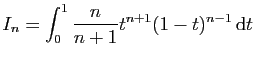
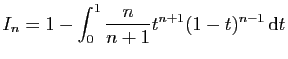
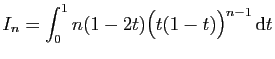
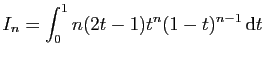
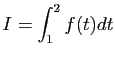
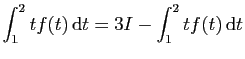
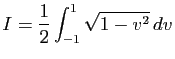
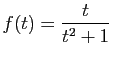
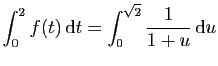
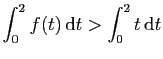
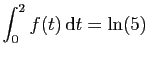
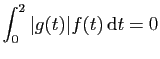
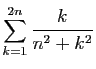
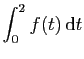
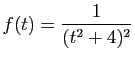
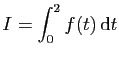
![$ I=\displaystyle{\frac{1}{8}\left(\int_0^2\frac{1}{t^2+4}
\mathrm{d}t+\left[\frac{t}{t^2+4}\right]_0^2
\right)}$](img562.gif)
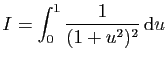
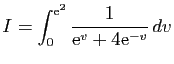
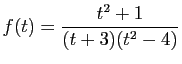
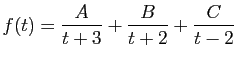
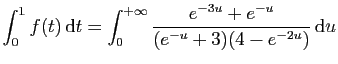
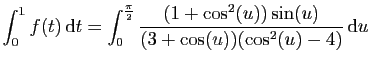
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales