Les théorèmes belges

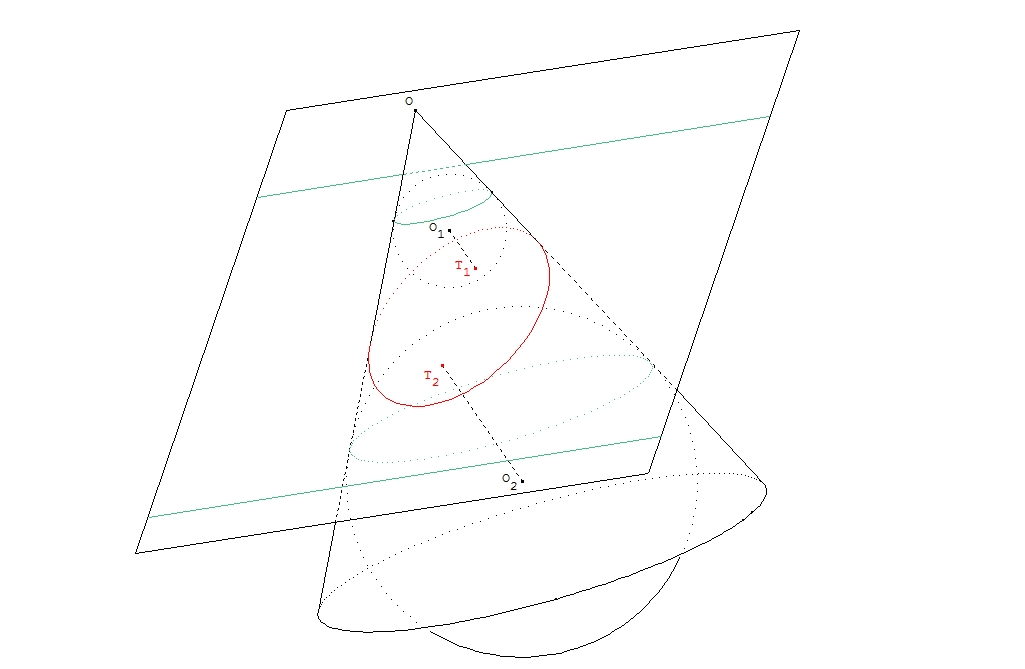
Alors que la définition et les propriétés des coniques étaient bien connues depuis l'antiquité grecque, ce n'est qu'au XIX^ième siècle que le théorème de Dandelin (1822) (ou de Dandelin-Quételet)¹ est venu caractériser les foyers et les directrices d'une conique obtenue comme section plane d'un cône de révolution.

Théorème 1   La section d'un cône de révolution par un plan est une conique dont les foyers sont les points de contact avec ce plan des deux sphères inscrites dans le cône et tangentes à ce plan et les directrices les intersections avec ce plan des deux plans contenant les cercles de contact de ces sphères avec le cône.

Dans le cas de l'ellipse, les deux sphères sont situées de part et d'autre du plan, dans le cas de l'hyperbole du même côté du plan de section. Dans le cas de la parabole, il n'y a qu'une sphère (et un couple foyer-directrice).

La figure ci-dessus représente le cas de l'ellipse : les deux sphères de centres $O_1$ et $O_2$ inscrites dans le cône sont tangentes en $T_1$ et $T_2$ au plan de section ; ces points sont les foyers de l'ellipse ; les directrices (représentées en vert) sont les intersections avec le plan de section des deux plans contenant les cercles de contact des deux sphères avec le cône.