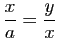 et
et
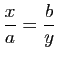 , de sorte que
, de sorte que 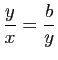 , ou encore
, ou encore
Les mathématiciens grecs étudiaient déjà les coniques, qu'ils définissaient comme sections planes des cônes de révolution. On attribue à Apollonius de Perge (v. 262-v. 190 av. J.-C.) l'introduction, dans son traité en huit volumes intitulé les Coniques, de la terminologie ellipse, hyperbole, parabole, mais ces termes étaient peut-être utilisés avant lui et beaucoup de propriétés de ces courbes étaient déjà connues. Ménechme (v. 380-v. 320 av.J.-C.) s'en servait pour tenter de résoudre le problème de la duplication du cube (voir le chapitre «Géométrie euclidienne»). En effet, si on veut introduire entre deux nombres ![]() et
et ![]() deux réels
deux réels ![]() et
et ![]() tels que
tels que ![]() constitue une progression géométrique, on a
constitue une progression géométrique, on a
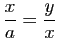 et
et
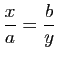 , de sorte que
, de sorte que ![]() et
et ![]() ; on est donc ramené à construire l'intersection d'une parabole et d'une hyperbole ; mais on peut aussi écrire
; on est donc ramené à construire l'intersection d'une parabole et d'une hyperbole ; mais on peut aussi écrire
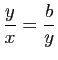 , ou encore
, ou encore ![]() et
et ![]() , ce qui amène à construire l'intersection de deux paraboles.
C'est à Pappus (290-350) qu'on attribue la définition des foyers et directrices, mais là encore ces notions étaient peut-être déjà connues avant lui.
, ce qui amène à construire l'intersection de deux paraboles.
C'est à Pappus (290-350) qu'on attribue la définition des foyers et directrices, mais là encore ces notions étaient peut-être déjà connues avant lui.
De fait, l'intersection d'un cône de révolution ![]() par un plan
par un plan ![]() ne passant pas par le sommet
ne passant pas par le sommet ![]() de
de ![]() est :
est :
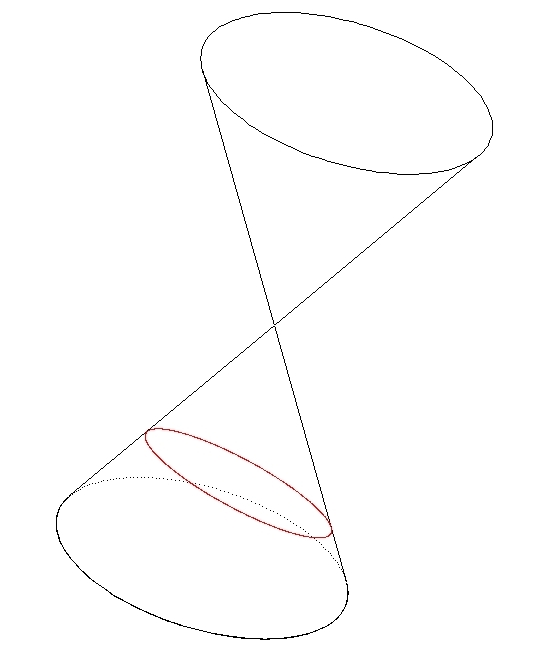
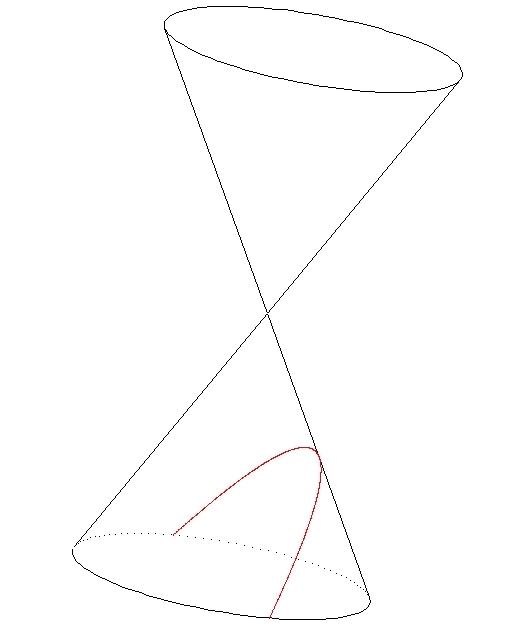
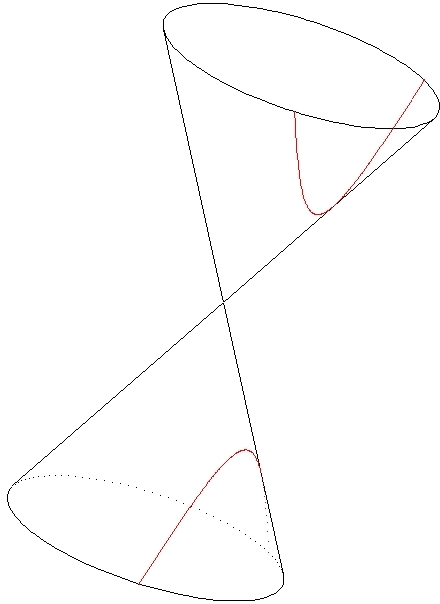
L'intersection d'un cylindre de révolution avec un plan est :
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales