Une application linéaire entre deux espaces de même dimension, si elle est injective, est aussi surjective, donc bijective.
Pour montrer que ![]() , on utilise encore l'associativité du
produit matriciel :
, on utilise encore l'associativité du
produit matriciel :
![]() . Or :
. Or :
Une application linéaire entre deux espaces de même dimension, si elle est injective, est aussi surjective, donc bijective.
Pour montrer que ![]() , on utilise encore l'associativité du
produit matriciel :
, on utilise encore l'associativité du
produit matriciel :
![]() . Or :
. Or :
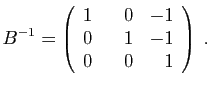
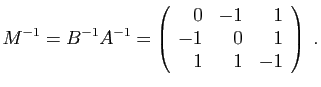
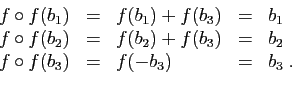
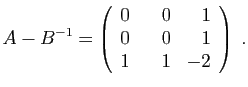
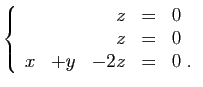
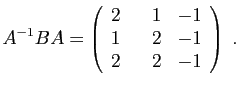
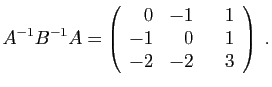
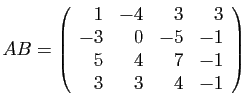 et
et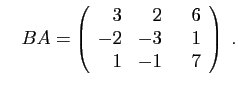
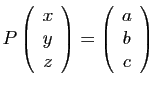 , on trouve que ce
système est de rang 3, donc la matrice
, on trouve que ce
système est de rang 3, donc la matrice
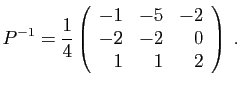
La matrice ![]() est celle de l'application composée
est celle de l'application composée ![]() . Puisque
. Puisque ![]() est de rang 2, l'image de
est de rang 2, l'image de ![]() est un plan vectoriel de
est un plan vectoriel de
![]() . Puisque l'application
. Puisque l'application ![]() est de rang 3, son noyau est
réduit à
est de rang 3, son noyau est
réduit à ![]() et sa restriction à
et sa restriction à
![]() est de rang 2. Donc l'image de
est de rang 2. Donc l'image de ![]() est un plan
vectoriel :
est un plan
vectoriel : ![]() est de rang 2.
est de rang 2.
Le raisonnement est analogue pour ![]() : c'est la matrice de
l'application
: c'est la matrice de
l'application ![]() . Puisque
. Puisque ![]() est de rang 3, son image est
est de rang 3, son image est
![]() , donc
, donc
![]() . Donc
. Donc ![]() est de rang 2, comme
est de rang 2, comme ![]() . Donc la matrice
. Donc la matrice ![]() est de rang 2.
est de rang 2.
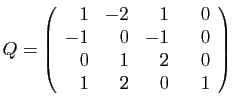 et
et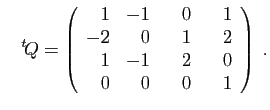
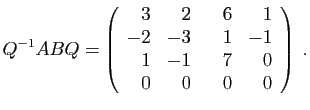
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales