Nous rappelons ici les liens entre les calculs sur les nombres
complexes et la géométrie du plan.
Le premier résultat concerne les mesures de distances et d'angles.
Théorème 7
Soient  ,
, 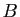 et
et 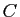 trois points distincts deux à deux, d'affixes
respectives
trois points distincts deux à deux, d'affixes
respectives 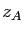 ,
, 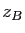 et
et 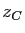 .
.
- La distance entre
 et
et 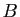 est le module de
est le module de 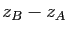 .
.
- L'angle orienté
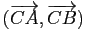 est
égal à l'argument du rapport
est
égal à l'argument du rapport
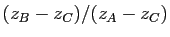 .
.
Si 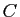 est un point du plan d'affixe
est un point du plan d'affixe 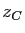 ,
et
,
et 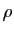 et un réel positif, l'ensemble
des points dont l'affixe
et un réel positif, l'ensemble
des points dont l'affixe  est telle que
est telle que
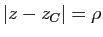 est le
cercle de centre
est le
cercle de centre 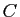 et de rayon
et de rayon 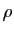 . On peut aussi écrire ce
cercle comme l'ensemble des points d'affixe
. On peut aussi écrire ce
cercle comme l'ensemble des points d'affixe
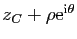 ,
où
,
où 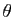 décrit
décrit 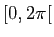 .
Comme conséquence immédiate du point 2, les points
.
Comme conséquence immédiate du point 2, les points 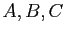 sont alignés si et seulement si l'argument de
sont alignés si et seulement si l'argument de
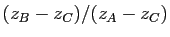 est égal à 0 ou
est égal à 0 ou 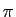 ; le triangle
; le triangle 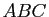 est rectangle en
est rectangle en 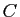 si
l'argument de
si
l'argument de
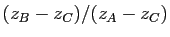 est égal à
est égal à 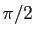 ou
ou
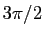 .
Voici maintenant la traduction sous forme de tranformations dans
.
Voici maintenant la traduction sous forme de tranformations dans
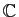 des translations, homothéties et rotations
(figure 5).
des translations, homothéties et rotations
(figure 5).
Théorème 8
Soit 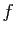 une application de
une application de
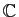 dans
dans
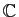 . On note
. On note 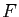 l'application du
plan dans lui-même qui au point d'affixe
l'application du
plan dans lui-même qui au point d'affixe  associe le point
d'affixe
associe le point
d'affixe 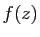 . Soit
. Soit  un point du plan, d'affixe
un point du plan, d'affixe 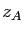 .
.
- Translation :
L'application
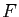 est la translation de vecteur
est la translation de vecteur
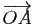 , si et seulement si
, si et seulement si 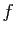 est l'application qui
à
est l'application qui
à  associe
associe 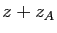 .
.
- Homothétie : Soit
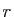 un réel.
L'application
un réel.
L'application 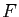 est l'homothétie de centre
est l'homothétie de centre  et de rapport
et de rapport
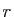 si et seulement si
si et seulement si 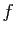 est l'application qui à
est l'application qui à  associe le
complexe
associe le
complexe 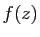 tel que
tel que
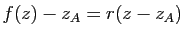 .
.
- Rotation : Soit
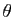 un réel.
L'application
un réel.
L'application 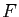 est la rotation de centre
est la rotation de centre  et d'angle
et d'angle
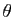 si et seulement si
si et seulement si 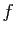 est l'application qui à
est l'application qui à  associe le
complexe
associe le
complexe 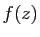 tel que
tel que
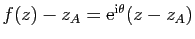 .
.
Figure 5:
Translation, homothétie et rotation dans le plan complexe.
|
|
Notons 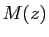 le point du plan d'affixe
le point du plan d'affixe  .
Si
.
Si  et
et 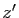 sont des nombres complexes,
le produit
sont des nombres complexes,
le produit 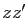 peut être décrit
comme l'unique nombre complexe
tel que le triangle
peut être décrit
comme l'unique nombre complexe
tel que le triangle
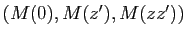 soit semblable au triangle
soit semblable au triangle
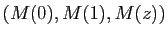 (figure 6).
(figure 6).
Figure 6:
Interprétation géométrique du produit de deux complexes.
|
|
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
 et
et 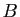 est le module de
est le module de 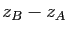 .
.
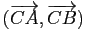 est
égal à l'argument du rapport
est
égal à l'argument du rapport
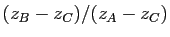 .
.
![]() le point du plan d'affixe
le point du plan d'affixe ![]() .
Si
.
Si ![]() et
et ![]() sont des nombres complexes,
le produit
sont des nombres complexes,
le produit ![]() peut être décrit
comme l'unique nombre complexe
tel que le triangle
peut être décrit
comme l'unique nombre complexe
tel que le triangle
![]() soit semblable au triangle
soit semblable au triangle
![]() (figure 6).
(figure 6).
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales