Equations résolubles par radicaux

On résout des équations du premier et du second degré au moins depuis les Babyloniens, au début du deuxième millénaire avant notre ère, mais ce n'est que depuis les XVI^e et surtout XVII^e siècles que zéro et les nombres négatifs sont traités de la même façon que les nombres positifs. Ainsi il y avait avant une théorie pour l'équation $x^2=ax+b$ et une autre pour $x^2+ax=b$, $a$ et $b$ étant supposés positifs.

Au début du IX^e siècle Al Khawarizmi (dont le nom a donné algorithme) décrit la méthode de résolution des équations du second degré, pratiquement telle que vous la connaissez (mais en supposant que le discriminant est positif ou nul). Il faudra attendre sept siècles et une belle bagarre avant que l'on sache résoudre les équations de degrés 3 et 4. Elle mit aux prises essentiellement deux mathématiciens italiens de la renaissance, Niccolò Fontana, dit Tartaglia (1499-1557) et Girolamo Cardano (1501-1576) (l'inventeur du joint de Cardan) : si vous êtes sages, nous vous la raconterons dans un autre chapitre.

Voici ce que l'on appelle de manière assez injuste les «formules de Cardan». Considérons l'équation :

$$(E)\qquad ax^3+bx^2+cx+d=0\;,$$

avec $a\neq 0$. En divisant par $a$ puis en posant $z=x+b/(3a)$, on obtient l'équation

$$(E')\qquad z^3+pz+q=0\;,$$

où

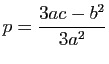$$p=\frac{3ac-b^2}{3a^2}$$   et$$\quad q=\frac{27a^2d-9abc+2b^3}{27a^3}\;.$$

Si $4p^3+27q^2\geqslant 0$, La formule suivante donne une solution réelle en $z$ :

$$z_0 = \sqrt[3]{-\frac{q}{2}+\frac{1}{2}\sqrt{\frac{4p^3+27q^2}{27}}} +\sqrt[3]{-\frac{q}{2}-\frac{1}{2}\sqrt{\frac{4p^3+27q^2}{27}}}\;.$$ (9)

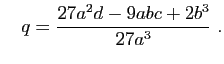
Tartaglia et Cardan n'utilisaient leurs formules que pour des équations dont on savait à l'avance qu'elles avaient des solutions réelles. Quand tout se passait bien, (9) donnait cette solution réelle. En factorisant par $(z-z_0)$, on se ramenait à une équation de degré $2$ que l'on savait résoudre.

Cardan, puis Bombelli furent intrigués par l'équation $x^3-15x-4=0$, dont $4$ est racine. Pourtant, la formule de Cardan donne comme solution

$$\sqrt[3]{2+11\sqrt{-1}}+\sqrt[3]{2-11\sqrt{-1}}\;.$$

En fait dans le cas général (9) définit six nombres complexes, parmi lesquels seulement trois sont solutions de l'équation $(E')$. En effet, si $u$ est tel que $u^3=z$, les deux autres racines cubiques de $z$ sont $ju$ et $\overline{j}u$, où $j=\mathrm{e}^{2\mathrm{i}\pi/3}$ et $\overline{j}=j^2=\mathrm{e}^{4\mathrm{i}\pi/3}$ sont les deux racines cubiques de l'unité différentes de $1$. Voici la solution complète de $(E')$.

1. Si $4p^3+27q^2\geqslant 0$, soient $u$ et $v$ les deux réels tels que
   $$u^3={-\frac{q}{2}+\frac{1}{2}\sqrt{\frac{4p^3+27q^2}{27}}}$$   et$$\quad v^3={-\frac{q}{2}-\frac{1}{2}\sqrt{\frac{4p^3+27q^2}{27}}}$$
   Les trois solutions de $(E')$ sont
   $$z_1=u+v\;,\quad z_2=ju+\overline{j}v\;,\quad z_3=\overline{j}u+jv\;.$$
   L'équation $(E')$ a une solution réelle, et deux solutions complexes conjuguées.
2. Si $4p^3+27q^2< 0$, soit $u$ un des complexes tels que :
   $$u^3={-\frac{q}{2}+\frac{\mathrm{i}}{2}\sqrt{\frac{-4p^3-27q^2}{27}}}\;.$$
   Les trois solutions de $(E')$ sont :
   $$z_1=u+\overline{u}\;,\quad z_2=ju+\overline{j}\overline{u}\;,\quad z_3=\overline{j}u+j\overline{u}\;.$$
   L'équation $(E')$ a trois solutions réelles, même s'il faut passer par les complexes pour les écrire.

En 1540, un élève de Cardan, Ludovico Ferrari donne des expressions explicites pour les solutions d'équations de degré 4, mais le problème des solutions non réelles demeure. En 1572, Bombelli surmonte sa répulsion à l'égard des racines carrées de nombres négatifs et écrit le nombre «più di meno», c'est-à-dire $\mathrm{i}$, puis définit les règles que vous connaissez, en particulier «più di meno via più di meno fa meno» : $\mathrm{i}\times \mathrm{i}=-1$. On constata bientôt qu'en acceptant les racines complexes et en comptant ces racines avec leur multiplicité, toute équation de degré 2 avait 2 racines, toute équation de degré 3 en avait 3 et toute équation de degré 4 en avait 4. Ceci fut énoncé par Girard en 1629, puis Descartes en 1637.

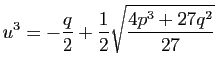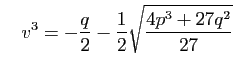
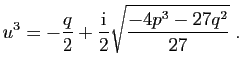
Et les équations de degré 5 ? On chercha longtemps une «résolution par radicaux» : une formule générale ne faisant intervenir que les opérations de $\mathbb{C}$ et l'extraction de racines. Le mémoire sur la résolution algébrique des équations que Joseph Louis Lagrange (1736-1813) publia en 1772 était une avancée importante. Il proposait une théorie ramenant le problème à l'étude des différentes valeurs que peuvent prendre certaines fonctions des racines lorsque l'on permute ces racines entre elles. Il y montrait aussi que les méthodes qui avaient conduit à la résolution des équations de degrés $2$ $3$ et $4$ ne pouvaient pas fonctionner sur une équation de degré $5$ générale. Il s'écoula encore 60 ans avant qu'Evariste Galois (1811-1832) ne comprenne que la résolubilité par radicaux était liée aux propriétés du groupe des permutations des racines. Une conséquence de la théorie de Galois était la démonstration du fait que les équations de degré 5 n'étaient pas résolubles par radicaux en général. Ce n'est qu'en 1870, avec la parution du «Traité des substitutions et des équations algébriques» de Camille Jordan (1838-1922) que l'ampleur des conceptions de Galois fut pleinement comprise.

Il faut dire que Galois avait exposé ses idées dans des articles plutôt mal écrits, souvent incomplets, ainsi que dans une lettre à un ami, fébrilement écrite dans la nuit du 29 mai 1832. Elle se terminait par ces mots : «Après cela, il y aura j'espère des gens qui trouveront leur profit à déchiffrer tout ce gâchis. Je t'embrasse avec effusion». Le lendemain matin, il mourait des suites d'un duel ; il avait 21 ans.