Voulez-vous calculer vos chances de gagner au Bridge, au Poker, au
Loto, au Keno ? Le procédure est à peu près la même et vous
avez tous les outils en main.
Commençons par une formule générale, qui vous servira pour
tous les jeux de hasard. Soit 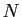 un entier au moins égal à
un entier au moins égal à
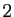 . Soient
. Soient 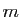 et
et 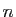 deux autres entiers inférieurs ou égaux à
deux autres entiers inférieurs ou égaux à
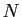 .
.
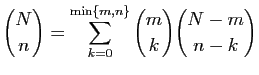 |
(8) |
On peut démontrer cette formule par récurrence, en utilisant les
propriétés des coefficients du binôme, mais il est plus
intéressant de la comprendre. Disons que 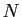 est un nombre d'objets
parmi lesquels vous vous apprêtez à en piocher
est un nombre d'objets
parmi lesquels vous vous apprêtez à en piocher 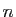 :
: 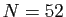 cartes et vous en recevez
cartes et vous en recevez 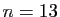 (Bridge) ;
(Bridge) ; 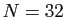 cartes et vous en
recevez
cartes et vous en
recevez 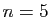 (Poker) ;
(Poker) ; 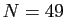 numéros et vous en cochez
numéros et vous en cochez
 (Loto) etc... Parmi les
(Loto) etc... Parmi les 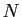 objets,
objets, 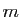 sont
marqués et ce sont ceux qui peuvent vous faire gagner :
sont
marqués et ce sont ceux qui peuvent vous faire gagner : 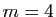 as au bridge,
as au bridge, 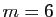 numéros du tirage officiel au loto, etc...
numéros du tirage officiel au loto, etc...
Vous avez
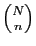 choix possibles. Ces choix se répartissent
selon le nombre d'objets marqués que vous aurez en main.
Il peut y en avoir au plus
choix possibles. Ces choix se répartissent
selon le nombre d'objets marqués que vous aurez en main.
Il peut y en avoir au plus
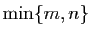 . Comment
constituer une sélection de
. Comment
constituer une sélection de 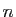 objets en tout, parmi lesquels
objets en tout, parmi lesquels 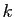 sont marqués ? Il faut choisir les
sont marqués ? Il faut choisir les 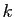 objets marqués parmi
objets marqués parmi 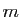 en
tout :
en
tout :
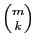 façons de le faire. Il faut ensuite choisir
façons de le faire. Il faut ensuite choisir
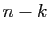 objets non marqués parmi
objets non marqués parmi 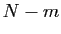 :
:
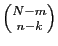 possibilités. La formule (8) traduit
cette décomposition.
possibilités. La formule (8) traduit
cette décomposition.
Comme cas particulier, voici comment décomposer le nombre de mains
au bridge (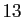 cartes distribuées sur
cartes distribuées sur 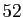 ) en fonction du
nombre d'as qu'elles contiennent.
) en fonction du
nombre d'as qu'elles contiennent.
Comment en déduire vos chances d'avoir 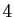 as dans une main ?
C'est facile, il suffit de diviser le nombre de mains contenant
as dans une main ?
C'est facile, il suffit de diviser le nombre de mains contenant 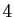 as
par le nombre total de mains.
as
par le nombre total de mains.
Le Rapido, comme son nom l'indique, ne demande pas une réflexion
très puissante, et les résultats défilent toutes les 10 minutes
sur un écran de télé. Pour jouer, vous cochez 8 numéros parmi
20 sur la grille A, et 1 numéro parmi 4 sur la grille B. Les
«bons» numéros affichés à la télé sont choisis de
même. Vous pouvez donc avoir 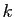 bons numéros (
bons numéros (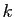 entre 0 et 8)
sur la grille A et 0 ou 1 sur la grille B. Vos chances d'avoir
entre 0 et 8)
sur la grille A et 0 ou 1 sur la grille B. Vos chances d'avoir 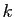 bons numéros sur la grille A sont de :
bons numéros sur la grille A sont de :
Pour avoir vos chances d'avoir en plus le bon numéro de la grille B,
multipliez par 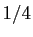 . Voici les probabilités pour
. Voici les probabilités pour 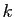 allant de 0 à 8
et
allant de 0 à 8
et 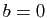 ou
ou 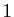 selon que vous avez ou non le numéro de la grille B.
selon que vous avez ou non le numéro de la grille B.
Vos chances d'avoir au moins 3 bons numéros sur la
grille A sont de 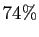 , ce qui vous encourage à jouer. Cependant
vous ne gagnez qu'à partir de 4 bons numéros.
Voici les gains en euros offerts pour 1 euro misé, pour
chacune des combinaisons gagnantes.
, ce qui vous encourage à jouer. Cependant
vous ne gagnez qu'à partir de 4 bons numéros.
Voici les gains en euros offerts pour 1 euro misé, pour
chacune des combinaisons gagnantes.
D'après les probabilités calculées plus haut, sur 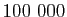 joueurs
payant chacun 1 euro, environ 6877 gagneront 1 euro, environ 7335
gagneront 2 euros, environ 2445 gagneront 6 euros, ... Au total,
la Française des Jeux reversera en moyenne
joueurs
payant chacun 1 euro, environ 6877 gagneront 1 euro, environ 7335
gagneront 2 euros, environ 2445 gagneront 6 euros, ... Au total,
la Française des Jeux reversera en moyenne 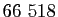 euros, pour
euros, pour
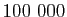 euros de mise empochés.
euros de mise empochés.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() un entier au moins égal à
un entier au moins égal à
![]() . Soient
. Soient ![]() et
et ![]() deux autres entiers inférieurs ou égaux à
deux autres entiers inférieurs ou égaux à
![]() .
.
![]() choix possibles. Ces choix se répartissent
selon le nombre d'objets marqués que vous aurez en main.
Il peut y en avoir au plus
choix possibles. Ces choix se répartissent
selon le nombre d'objets marqués que vous aurez en main.
Il peut y en avoir au plus
![]() . Comment
constituer une sélection de
. Comment
constituer une sélection de ![]() objets en tout, parmi lesquels
objets en tout, parmi lesquels ![]() sont marqués ? Il faut choisir les
sont marqués ? Il faut choisir les ![]() objets marqués parmi
objets marqués parmi ![]() en
tout :
en
tout :
![]() façons de le faire. Il faut ensuite choisir
façons de le faire. Il faut ensuite choisir
![]() objets non marqués parmi
objets non marqués parmi ![]() :
:
![]() possibilités. La formule (8) traduit
cette décomposition.
possibilités. La formule (8) traduit
cette décomposition.
![]() cartes distribuées sur
cartes distribuées sur ![]() ) en fonction du
nombre d'as qu'elles contiennent.
) en fonction du
nombre d'as qu'elles contiennent.
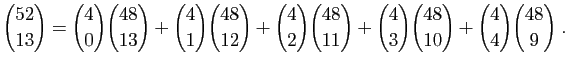
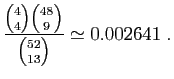
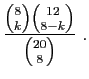

![]() , ce qui vous encourage à jouer. Cependant
vous ne gagnez qu'à partir de 4 bons numéros.
Voici les gains en euros offerts pour 1 euro misé, pour
chacune des combinaisons gagnantes.
, ce qui vous encourage à jouer. Cependant
vous ne gagnez qu'à partir de 4 bons numéros.
Voici les gains en euros offerts pour 1 euro misé, pour
chacune des combinaisons gagnantes.
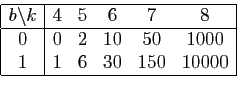
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales