Les formules de Ramanujan

Srinivasa Ramanujan (1887-1920) avait appris tout seul les mathématiques, grâce à deux livres seulement. Admis en 1903 dans un collège gouvernemental du sud de l'Inde, il était tellement obnubilé par ses recherches qu'il échoua à ses examens, et ce quatre ans de suite. Ayant obtenu un poste dans un comptoir de Madras, ses supérieurs l'encouragèrent à envoyer ses résultats à d'éminents mathématiciens anglais. Seul G.H. Hardy (1877-1947) fit l'effort de s'intéresser à la lettre qu'il reçut le 16 janvier 1913, et qui contenait 120 formules. L'écriture mathématique était particulière et aucune justification n'était fournie. Ramanujan n'aura d'ailleurs jamais une idée claire de ce qu'est une démonstration. Il disait : «une équation pour moi n'a aucun sens, à moins qu'elle n'exprime une pensée de Dieu».

Après quelques heures d'effort, Hardy reconnut certaines formules ; d'autres étaient erronées. Mais un grand nombre étaient totalement nouvelles. Hardy déclara «un coup d' $\oe$ il sur ces formules était suffisant pour se rendre compte qu'elles ne pouvaient être pensées que par un mathématicien de la plus grande classe. Elles devaient être vraies, car si elles ne l'étaient pas, personne n'aurait eu assez d'imagination pour les inventer».

Hardy invita Ramanujan à Cambridge où il séjourna de 1914 à 1919. Au fil du temps, la santé de Ramanujan déclinait, et son régime strictement végétarien ainsi que les restrictions dues à la première guerre mondiale ne l'amélioraient pas. Il retourna en Inde, ou il mourut à seulement 32 ans. Personne, pas même Hardy, n'avait eu le temps de comprendre d'où lui venaient ses intuitions géniales. Il fit dans sa vie environ 6000 découvertes qu'il consignait dans des carnets. Le déchiffrage de ces carnets a occupé de nombreux mathématiciens tout au long du XX^e siècle.

Voici une des nombreuses formules que Ramanujan donna pour le calcul de $\pi$ : elle date de 1910 mais ne fut démontrée qu'en 1985.

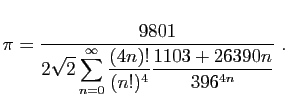
$\displaystyle \pi = \frac{9801}{\displaystyle{2\sqrt{2}\sum_{n=0}^\infty \frac{(4n)!}{(n!)^4}\frac{1103+26390n}{396^{4n}}}}\;.$