Par des arguments d'arithmétique élémentaire, il est facile de prouver
qu'il n'existe pas de carré de côté de longueur rationnelle dont
l'aire est égale à 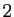 : l'équation
: l'équation 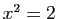 n'a pas de solution
dans
n'a pas de solution
dans
 . Néanmoins, il existe une infinité de suites de
rationnels
. Néanmoins, il existe une infinité de suites de
rationnels
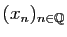 , telles que
, telles que 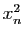 converge vers
converge vers
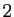 . C'est le cas par exemple, pour toute suite définie par
. C'est le cas par exemple, pour toute suite définie par
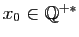 et:
et:
(Démontrez-le !) Une conséquence est que la suite
 ne converge pas dans
ne converge pas dans
 .
.
Sans perdre de propriétés algébriques, nous allons
construire un nouveau corps
 totalement ordonné
contenant
totalement ordonné
contenant
 et dans lequel toutes les suites qui devraient
naturellement converger (ce seront les suites de Cauchy) seront
effectivement convergentes.
et dans lequel toutes les suites qui devraient
naturellement converger (ce seront les suites de Cauchy) seront
effectivement convergentes.
Définition 7
Soit
 une suite d'éléments de
une suite d'éléments de
 , c'est-à-dire une
application de
, c'est-à-dire une
application de
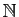 dans
dans
 .
.
- (i)
- La suite
 est bornée s'il existe
est bornée s'il existe
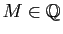 tel que
tel que
- (ii)
- La suite
 converge dans
converge dans
 vers
vers
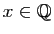 si
si
- (iii)
- La suite
 est de Cauchy dans
est de Cauchy dans
 si
si
Démonstration :
- 1.
- Soit
 une suite qui converge dans
une suite qui converge dans
 vers
vers
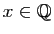 , alors pour
, alors pour
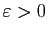 ,
,
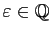 , il existe
, il existe
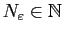 tel que pour tout
tel que pour tout
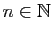
Par conséquent pour
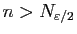 et
et
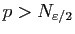 on
a
on
a
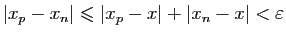 et la suite
et la suite
 est donc de Cauchy dans
est donc de Cauchy dans
 .
.
- 2.
- Soit
 une suite de Cauchy dans
une suite de Cauchy dans
 , alors
, alors
En prenant
 on obtient que si
on obtient que si 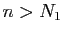 on a
on a
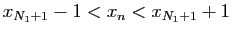 . Par conséquent si on pose
. Par conséquent si on pose
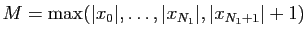 , pour tout
, pour tout
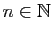 ,
,
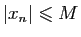 et la suite
et la suite
 est bornée.
est bornée.
- 3.
- Soit
 une suite qui converge dans
une suite qui converge dans
 vers 0
et
vers 0
et
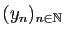 une suite bornée, alors pour
une suite bornée, alors pour
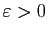 ,
,
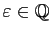 , il existe
, il existe
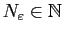 tel que pour tout
tel que pour tout
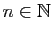
et il existe 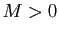 ,
,
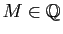 , tel que pour tout
, tel que pour tout
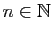
On en déduit que si
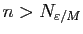 alors
alors
Les assertions 4) et 5) pour les sommes et les différences de suites
sont des conséquences immédiates de l'inégalité triangulaire et des
définitions et leur démonstration est laissée au lecteur. Prouvons 4)
pour le produit, la démonstration de 5) pour le produit est
analogue. Soient
 et
et
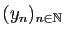 deux suites de
Cauchy, alors pour
deux suites de
Cauchy, alors pour
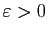 ,
,
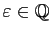 , il existe
, il existe
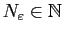 et
et
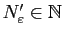 tels que pour tout
tels que pour tout
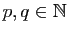
De plus, d'après 2), il existe 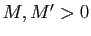 ,
,
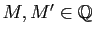 , tels que pour
tout
, tels que pour
tout
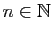
On en déduit que, pour tout
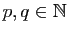 ,
,
Posons
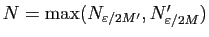 , alors si
, alors si 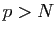 et
et 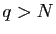 on a
on a
- 6.
- Soit
 une suite de Cauchy ne convergeant pas vers 0, alors
une suite de Cauchy ne convergeant pas vers 0, alors
La suite
 étant de Cauchy, il existe
étant de Cauchy, il existe
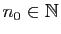 tel que
tel que
En prenant 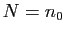 ,
, 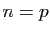 alors pour tout
alors pour tout 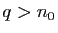 on a
on a
soit
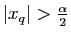 grâce à l'inégalité triangulaire, d'où
grâce à l'inégalité triangulaire, d'où
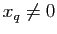 si
si 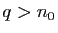 .
Soient
.
Soient 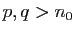 , alors
, alors
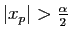 et
et
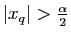 ,
d'où
,
d'où
Donc puisque
 est une suite de Cauchy, la suite
est une suite de Cauchy, la suite
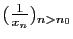 est de Cauchy.
est de Cauchy.

Dans
 , il existe des suites de Cauchy non
convergentes. Nous en avons vu des exemples plus haut. En voici un
autre.
Considérons la suite
, il existe des suites de Cauchy non
convergentes. Nous en avons vu des exemples plus haut. En voici un
autre.
Considérons la suite
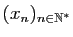 définie par
définie par
Si 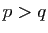 , on a
, on a
Pour
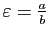 ,
,
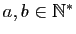 ,
, 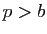 et
et 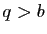 implique
implique
Cette suite est donc de Cauchy, mais ne converge pas vers un nombre
rationnel
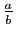 . Supposons qu'elle converge vers
. Supposons qu'elle converge vers
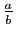 . Puisque l'inégalité
. Puisque l'inégalité
est valable pour tout 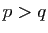 , en faisant tendre
, en faisant tendre 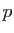 vers l'infini on aurait
vers l'infini on aurait
la première inégalité restant stricte puisque la suite
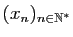 est croissante. Par définition de
est croissante. Par définition de 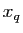 , si
, si
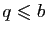 , le nombre rationnel
, le nombre rationnel
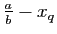 peut être représenté par une
fraction de la forme
peut être représenté par une
fraction de la forme
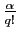 ,
,
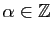 , et donc
, et donc
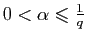 , ce qui est impossible si
, ce qui est impossible si 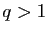 .
.
On peut également considérer la suite
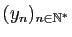 définie par
définie par
La suite
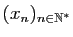 est clairement croissante et la suite
est clairement croissante et la suite
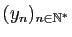 est décroissante
puisque
est décroissante
puisque
De plus la suite
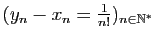 est une suite de
rationnels positifs qui converge vers 0 et pour tous
est une suite de
rationnels positifs qui converge vers 0 et pour tous
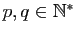 on a
on a
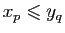 . Par conséquent si ces suites convergeaient leurs
limites seraient égales et cette limite
. Par conséquent si ces suites convergeaient leurs
limites seraient égales et cette limite 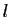 vérifierait
vérifierait
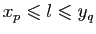 pour tous
pour tous
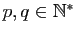 .
.
On aimerait alors compléter
 en un nouvel ensemble ordonné de
nombres dans lequel toute suite de Cauchy serait convergente. Les deux
suites
en un nouvel ensemble ordonné de
nombres dans lequel toute suite de Cauchy serait convergente. Les deux
suites
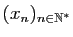 et
et
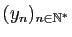 précédentes auraient
alors une limite commune dans cet ensemble qui serait située entre
chacun des nombres rationnels
précédentes auraient
alors une limite commune dans cet ensemble qui serait située entre
chacun des nombres rationnels 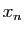 et
et 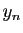 .
Nous allons construire un tel ensemble.
.
Nous allons construire un tel ensemble.
Précisons tout d'abord les propriétés souhaitées pour le nouvel
ensemble de nombres que nous souhaitons construire.
Nous allons construire un corps commutatif noté
 contenant
contenant
 et qui sera archimédien et complet comme quotient de l'ensemble des
suites de Cauchy de
et qui sera archimédien et complet comme quotient de l'ensemble des
suites de Cauchy de
 .
.
Notons
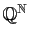 l'ensemble des suites de rationnels, c'est-à-dire
l'ensemble des applications de
l'ensemble des suites de rationnels, c'est-à-dire
l'ensemble des applications de
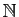 dans
dans
 , et
, et
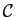 le
sous-ensemble de
le
sous-ensemble de
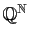 constitué des suites de Cauchy.
constitué des suites de Cauchy.
Grâce à la propriété 4) des suites de rationnels
l'ensemble
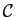 des
suites de Cauchy dans
des
suites de Cauchy dans
 est muni d'une structure d'anneau
commutatif si on pose pour
est muni d'une structure d'anneau
commutatif si on pose pour
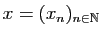 et
et
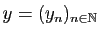
l'élément neutre de 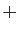 est
est 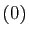 , la suite stationnaire nulle et
l'élément neutre de
, la suite stationnaire nulle et
l'élément neutre de  est
est 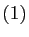 la suite stationnaire
d'éléments égaux à
la suite stationnaire
d'éléments égaux à 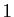 .
.
Proposition 19
L'ensemble
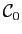 des suites de rationnels qui convergent vers 0
est un idéal de
des suites de rationnels qui convergent vers 0
est un idéal de
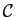 .
.
Démonstration : Le fait que
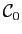 soit un sous-groupe additif de
soit un sous-groupe additif de
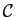 est une
conséquence directe des propriétés 1) et 5) des suites de
rationnels. Pour prouver que
est une
conséquence directe des propriétés 1) et 5) des suites de
rationnels. Pour prouver que
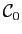 est un idéal de
est un idéal de
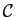 , il reste à
montrer que si
, il reste à
montrer que si
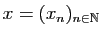 est un élément de
est un élément de
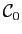 et si
et si
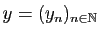 est une suite Cauchy de rationnels alors
est une suite Cauchy de rationnels alors
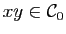 . Cela résulte immédiatement des
propriétés 2) et 3) des
suites de rationnels.
. Cela résulte immédiatement des
propriétés 2) et 3) des
suites de rationnels. 
Définition 9
L'anneau quotient
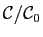 est appelé
droite numérique et
noté
est appelé
droite numérique et
noté
 . Ses éléments sont appelés nombres réels.
. Ses éléments sont appelés nombres réels.
Proposition 20
 est un corps commutatif.
est un corps commutatif.
Démonstration :
 est un anneau commutatif qui admet pour unité la classe
est un anneau commutatif qui admet pour unité la classe
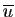 des suites qui convergent vers
des suites qui convergent vers 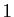 . Il reste à prouver que si une
suite de Cauchy
. Il reste à prouver que si une
suite de Cauchy
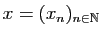 ne converge pas vers 0, il
existe une suite de Cauchy
ne converge pas vers 0, il
existe une suite de Cauchy
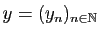 telle que
telle que 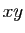 converge
vers
converge
vers 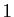 . Par la propriété 6) des suites de rationnels, si
. Par la propriété 6) des suites de rationnels, si 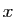 ne
converge pas vers 0 il existe un entier
ne
converge pas vers 0 il existe un entier 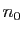 tel que la suite
tel que la suite
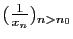 est de Cauchy. Posons
est de Cauchy. Posons 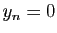 si
si
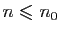 et
et
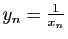 si
si 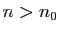 , la suite
, la suite
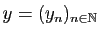 ainsi
construite est telle que la suite
ainsi
construite est telle que la suite 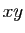 converge vers
converge vers 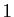 . Ainsi on a
. Ainsi on a
ce qui prouve, puisque
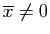 si et seulement si
si et seulement si
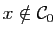 , que tout élément non nul de
, que tout élément non nul de
 possède un inverse
dans
possède un inverse
dans
 .
. 
Proposition 21
On définit un isomorphisme 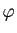 de
de
 sur un sous-corps de
sur un sous-corps de
 en associant à chaque rationnel
en associant à chaque rationnel 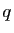 la classe
la classe
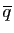 constituée
des suites de rationnels qui convergent vers
constituée
des suites de rationnels qui convergent vers 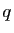 .
.
Démonstration : Il résulte immédiatement de la propriété 4) des suites de rationnels
que 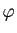 est un homomorphisme d'anneau. De plus puisque
est un homomorphisme d'anneau. De plus puisque
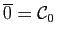 ,
,
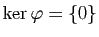 et
et 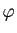 est donc injectif. Il
définit donc un isomorphisme de
est donc injectif. Il
définit donc un isomorphisme de
 sur un sous-corps de
sur un sous-corps de
 .
. 
Relation d'ordre dans
 Soit
Soit
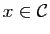 une suite de Cauchy de rationnels, on dira que
une suite de Cauchy de rationnels, on dira que
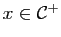 si et seulement si
si et seulement si
et que
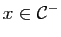 si et seulement si
si et seulement si
Démonstration : Soient
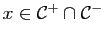 , pour
, pour
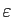 donné il existe
donné il existe
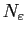 et
et
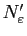 tels que si
tels que si
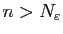 et
et
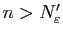 on ait respectivement
on ait respectivement
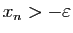 et
et
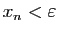 , d'où si
, d'où si
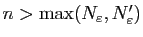 on
aura
on
aura
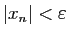 , c'est-à-dire
, c'est-à-dire
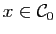 .
.
Soit
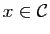 , alors
, alors
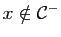 équivaut à
équivaut à
Puisque 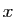 est une suite de Cauchy, il existe
est une suite de Cauchy, il existe 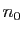 tel que si
tel que si
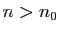 et
et 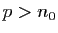 on a
on a
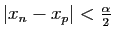 . Choisissons
. Choisissons
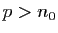 tel que
tel que
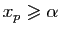 , alors pour tout
, alors pour tout 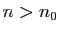 on a
on a
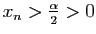 et donc
et donc
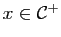 .
. 
Démonstration : Les assertions (i) et (ii) sont des conséquences directes de la
définition de
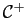 . Considérons l'assertion (iii) : si
parmi
. Considérons l'assertion (iii) : si
parmi 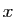 et
et
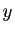 l'un est dans
l'un est dans
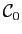 , alors
, alors
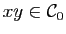 par les
propriétés 2) et
3) des suites de rationnels et si
par les
propriétés 2) et
3) des suites de rationnels et si 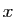 et
et 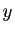 ne sont pas dans
ne sont pas dans
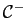 ,
pour
,
pour 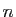 assez grand on a
assez grand on a 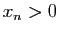 et
et 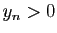 et donc
et donc 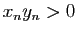 , soit
, soit
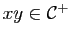 , ce qui prouve (iii).
, ce qui prouve (iii).
Pour l'assertion (iv) considérons le cas où
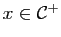 , le cas où
, le cas où
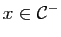 se traite de manière analogue. Si
se traite de manière analogue. Si
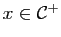 et si
et si
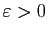 ,
,
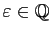 est donné, il existe
est donné, il existe 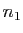 tel
que
tel
que
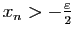 si
si 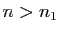 . Comme
. Comme
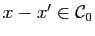 , il
existe
, il
existe 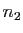 tel que si
tel que si 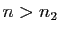 alors
alors
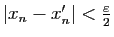 . Ainsi pour
. Ainsi pour
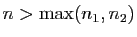 on a
on a
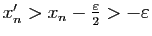 , c'est-à-dire
, c'est-à-dire
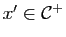 .
. 
L'assertion (iv) du Lemme 3 permet de donner la
définition suivante :
Les Lemmes 2 et 3 permettent de définir une
relation d'ordre sur
 en posant
en posant
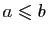 si et seulement si
si et seulement si
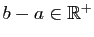 . Grâce aux propriétés (i), (ii) et (iii) du Lemme
3,
. Grâce aux propriétés (i), (ii) et (iii) du Lemme
3,
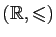 est un corps totalement
ordonné. Notons que l'injection
est un corps totalement
ordonné. Notons que l'injection 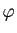 de
de
 dans
dans
 est
croissante, puisque
est
croissante, puisque
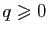 dans
dans
 équivaut à
équivaut à
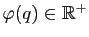 .
.
Démonstration : Il suffit de prouver que pour tout
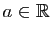 , il existe
, il existe
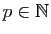 tel
que
tel
que 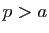 (si
(si
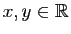 avec
avec 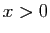 , en posant
, en posant
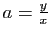 on
aura
on
aura 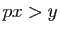 ). Soit
). Soit
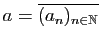 . La suite
. La suite
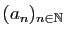 étant de Cauchy, elle est bornée et par conséquent
il existe
étant de Cauchy, elle est bornée et par conséquent
il existe
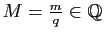 tel que
tel que
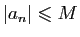 pour tout
pour tout
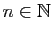 . La suite
. La suite
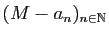 est constituée de rationnels
positifs, elle est donc dans
est constituée de rationnels
positifs, elle est donc dans
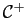 , ce qui signifie que le nombre
réel M-a est positif. On a donc
, ce qui signifie que le nombre
réel M-a est positif. On a donc
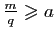 , d'où
, d'où
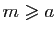 et
et
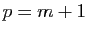 convient.
convient. 
Notion de suite de Cauchy et de suite convergente
dans
 Les définitions sont analogues à celles des suites de Cauchy et des
suites convergentes dans
Les définitions sont analogues à celles des suites de Cauchy et des
suites convergentes dans
 , mais cette fois on autorise
, mais cette fois on autorise
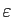 à appartenir à
à appartenir à
 . Comme
. Comme
 est archimédien cela
n'apporte rien car si
est archimédien cela
n'apporte rien car si
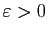 est un nombre réel, il existe
est un nombre réel, il existe
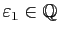 tel que
tel que
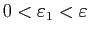 (il suffit
de poser
(il suffit
de poser
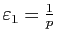 , avec
, avec
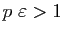 ).
).
Pour prouver que
 est complet nous avons besoin de quelques
lemmes qui ont un intérêt intrinsèque.
est complet nous avons besoin de quelques
lemmes qui ont un intérêt intrinsèque.
Lemme 4
Si 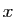 et
et 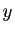 sont deux éléments de
sont deux éléments de
 tels que
tels que 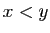 , il existe
, il existe
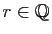 tel que
tel que 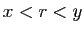 .
.
Démonstration : Puisque
 est archimédien, il existe
est archimédien, il existe
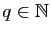 tel que
tel que 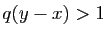 .
Soit
.
Soit
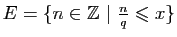 . Comme
. Comme
 est archimédien
et
est archimédien
et
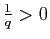 , il existe
, il existe
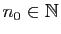 tel que
tel que
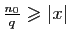 , par conséquent l'ensemble
, par conséquent l'ensemble 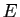 n'est pas vide car il contient
n'est pas vide car il contient
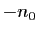 et il est majoré par
et il est majoré par 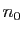 ; il possède donc un plus grand
élément
; il possède donc un plus grand
élément 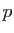 qui vérifie
qui vérifie
Posons
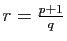 , alors
, alors
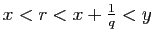 par définition de
par définition de 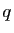 .
.
Lemme 5
Toute suite de Cauchy de rationnels converge dans
 vers le nombre
réel qu'elle représente.
vers le nombre
réel qu'elle représente.
Démonstration : Soit
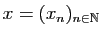 une suite de Cauchy dans
une suite de Cauchy dans
 . Choisissons
. Choisissons
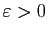 ,
,
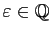 , il existe alors
, il existe alors
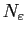 tel que si
tel que si
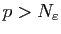 et
et
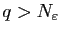 on a
on a
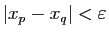 , c'est-à-dire
, c'est-à-dire
Fixons
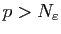 , par définition de la relation d'ordre sur
, par définition de la relation d'ordre sur
 on obtient
on obtient
ce qui implique que la suite
 converge vers
converge vers
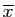 dans
dans
 .
.
Démonstration : Soit
 une suite de Cauchy dans
une suite de Cauchy dans
 . Nous allons
construire une suite
. Nous allons
construire une suite
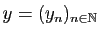 de rationnels assez «proche»
de la suite
de rationnels assez «proche»
de la suite
 pour qu'elle soit encore de Cauchy et
nous montrerons que la suite
pour qu'elle soit encore de Cauchy et
nous montrerons que la suite
 converge vers
converge vers
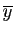 dans
dans
 .
.
Construction de la suite
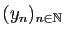
Pour tout
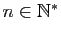 , il résulte du Lemme 4 qu'il existe
, il résulte du Lemme 4 qu'il existe
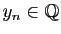 tel que
tel que
Pour
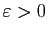 ,
,
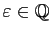 donné, il existe
donné, il existe
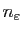 tel que si
tel que si
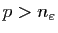 et
et
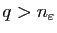 on a
on a
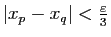 et donc
et donc
Posons
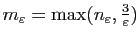 ,
alors si
,
alors si
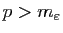 et
et
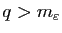 on a
on a
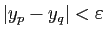 . La suite
. La suite
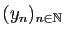 est donc de Cauchy
dans
est donc de Cauchy
dans
 .
.
Convergence de la suite

Il résulte de la démonstration du Lemme 5 que
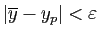 si
si
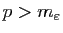 , d'où
, d'où
et la suite
 converge donc vers
converge donc vers
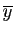 .
. Représentation décimale d'un nombre réel
L'objet de ce paragraphe est de prouver que, pour tout
Représentation décimale d'un nombre réel
L'objet de ce paragraphe est de prouver que, pour tout
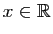 , il
existe une unique suite
, il
existe une unique suite
 d'éléments de
d'éléments de
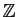 tels
que, pour tout
tels
que, pour tout
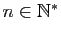 ,
,
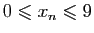 et pour tout
et pour tout
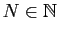 il existe
il existe
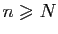 tel que
tel que 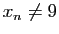 et
et
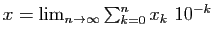 . La suite
. La suite
 est unique. La suite
est unique. La suite
 s'appelle un
développement décimal propre de
s'appelle un
développement décimal propre de 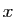 et il est d'usage de le
noter
et il est d'usage de le
noter
Lemme 6
Pour tout
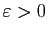 et tout
et tout
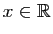 , il existe un unique
entier
, il existe un unique
entier
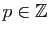 tel que
tel que
Démonstration : Comme
 est archimédien, il existe
est archimédien, il existe
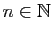 tel que
tel que
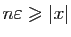 , i.e.
, i.e.
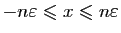 ,
donc l'ensemble
,
donc l'ensemble 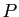 des entiers relatifs tels que
des entiers relatifs tels que
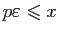 est non vide (
est non vide (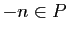 ) et majoré par
) et majoré par 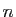 , il admet donc un plus
grand élément
, il admet donc un plus
grand élément 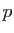 qui vérifie bien sûr
qui vérifie bien sûr
Si 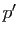 vérifiait également
vérifiait également
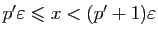 , on aurait
, on aurait
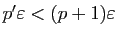 et
et
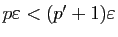 ,
d'où
,
d'où 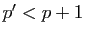 et
et 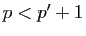 puisque
puisque
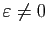 , soit
, soit 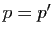 .
. 
Lorsque
 , l'entier
, l'entier 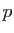 du Lemme 6
s'appelle la partie entière de
du Lemme 6
s'appelle la partie entière de 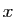 et est habituellement
noté
et est habituellement
noté
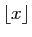 . On appelle partie décimale
de
. On appelle partie décimale
de 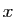 la différence
la différence
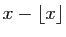 . On la note
. On la note 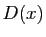 ,
elle appartient à l'intervalle
,
elle appartient à l'intervalle 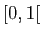 .
.
Soit
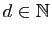 ,
,
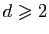 , prenons
, prenons
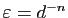 . Si
. Si
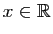 , d'après le Lemme 6, il existe un unique
, d'après le Lemme 6, il existe un unique
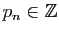 tel que
tel que
Le nombre rationnel
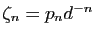 s'appelle la valeur
approchée par défaut de
s'appelle la valeur
approchée par défaut de 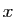 à
à 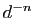 près.
près.
En remplaçant 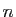 par
par 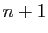 , on obtient
, on obtient 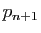 qui vérifie
qui vérifie
d'où
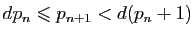 . On peut alors définir par récurrence
une unique suite
. On peut alors définir par récurrence
une unique suite
 telle que
telle que
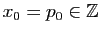 et
et
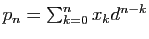 avec
avec
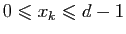 si
si
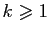 . La
valeur approchée par défaut de
. La
valeur approchée par défaut de 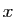 à
à 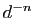 près est alors donnée
par
près est alors donnée
par
Remarquons que, puisque
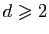 ,
,
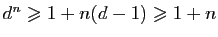 par la
formule du binôme de Newton donc
par la
formule du binôme de Newton donc
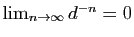 . La
suite
. La
suite
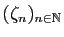 des valeurs approchées vérifie
des valeurs approchées vérifie
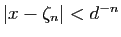 et converge donc vers
et converge donc vers 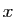 quand
quand 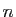 tend vers
l'infini.
tend vers
l'infini.
Lorsque 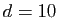 la suite
la suite
 s'appelle un
développement décimal illimité de
s'appelle un
développement décimal illimité de 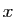 et on écrit
et on écrit
On dira que le développement décimal est propre si, pour tout
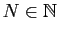 , il existe
, il existe
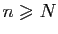 tel que
tel que 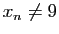 . Les développements
obtenus par la méthode développée ici sont toujours propres. En effet
si
. Les développements
obtenus par la méthode développée ici sont toujours propres. En effet
si 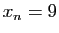 pour tout
pour tout 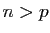 , on aurait
, on aurait
et
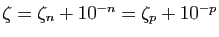 pour tout
pour tout 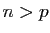 , mais
, mais
par définition de 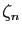 , soit
, soit
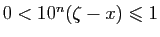 pour tout
pour tout
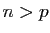 ce qui est impossible puisque
ce qui est impossible puisque
 est archimédien.
est archimédien.
Nous venons donc de prouver que tout nombre réel 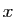 possède un unique
développement décimal illimité propre. Si on note
possède un unique
développement décimal illimité propre. Si on note
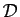 l'ensemble
des suites
l'ensemble
des suites
 d'entiers relatifs telles que pour tout
d'entiers relatifs telles que pour tout
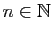 ,
,
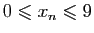 et pour tout
et pour tout
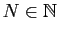 il
existe
il
existe
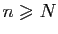 tel que
tel que 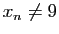 , nous avons donc défini une application
, nous avons donc défini une application
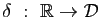 qui a chaque nombre réel
qui a chaque nombre réel 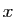 associe son
développement décimal illimité propre.
associe son
développement décimal illimité propre.
Démonstration : L'existence de l'application 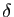 et la formule (10)
résultent de ce qui précède. Il reste à prouver que
et la formule (10)
résultent de ce qui précède. Il reste à prouver que 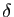 est une
bijection.
Soit
est une
bijection.
Soit
 un élément de
un élément de
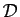 , cherchons
, cherchons
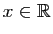 tel
que
tel
que
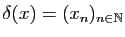 . Remarquons que la suite de rationnels
. Remarquons que la suite de rationnels
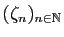 définie par
définie par
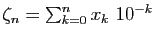 est croissante et de Cauchy. En effet
est croissante et de Cauchy. En effet
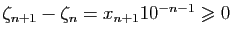 et si
et si 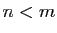
La suite de rationnels
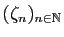 définit donc un nombre
réel
définit donc un nombre
réel 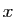 . De plus si on pose
. De plus si on pose
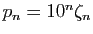 ,
,
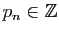 et
et
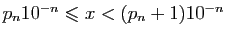 , et par conséquent
, et par conséquent
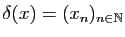 par construction de
par construction de 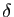 .
.
Notons 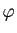 l'application de
l'application de
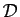 dans
dans
 qui à la suite
qui à la suite
 associe le nombre réel
associe le nombre réel 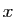 défini par la suite
défini par la suite
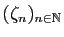 , il est clair que
, il est clair que
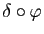 et
et
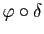 sont respectivement l'application identique de
sont respectivement l'application identique de
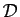 et celle de
et celle de
 , ce qui prouve que
, ce qui prouve que 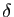 est bijective et
que
est bijective et
que
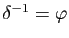 .
. 
La proposition suivante permet de caractériser nombres rationnels par
leurs développements décimaux.
Proposition 23
L'ensemble
 des nombres rationnels correspond au sous-ensemble
des nombres réels dont le développement décimal est périodique.
des nombres rationnels correspond au sous-ensemble
des nombres réels dont le développement décimal est périodique.
Démonstration : Soit
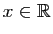 un nombre réel dont le développement décimal est
périodique,i.e.
un nombre réel dont le développement décimal est
périodique,i.e.
Alors
et par conséquent
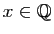 .
.
Réciproquement soit
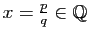 avec
avec 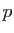 et
et 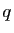 des entiers
premiers entre eux. On définit par récurrence une suite d'entiers
des entiers
premiers entre eux. On définit par récurrence une suite d'entiers
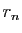 ,
,
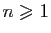 , tels que
, tels que
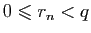 en considérant
les restes des
divisions euclidiennes successives de
en considérant
les restes des
divisions euclidiennes successives de 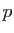 par
par 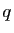 , puis de
, puis de 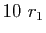 par
par 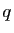 et ainsi de suite. En notant
et ainsi de suite. En notant 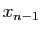 les différents
quotients on aura
les différents
quotients on aura
La suite
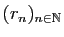 prenant ses valeurs dans un ensemble fini à
prenant ses valeurs dans un ensemble fini à
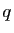 éléments, les nombres
éléments, les nombres
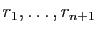 ne peuvent pas être
deux à deux distincts. Si
ne peuvent pas être
deux à deux distincts. Si 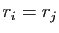 pour
pour
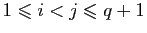 , la suite
, la suite
 vérifie
vérifie
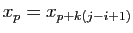 pour
pour
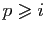 et
et
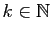 , elle est donc périodique.
, elle est donc périodique.
De plus
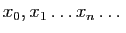 est le développement décimal de
est le développement décimal de 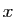 car
car
puisque 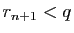 .
.
Grâce aux développement décimaux on peut montrer que
 , qui
contient
, qui
contient
 , est en fait beaucoup plus gros que
, est en fait beaucoup plus gros que
 .
.
Proposition 24
L'ensemble
 n'est pas dénombrable.
n'est pas dénombrable.
Démonstration : Nous allons démontrer que l'intervalle
![$ [0,1]\subset\mathbb{R}$](img928.gif) n'est pas
dénombrable. Il suffit de prouver que pour tout sous-ensemble
dénombrable
n'est pas
dénombrable. Il suffit de prouver que pour tout sous-ensemble
dénombrable 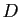 de
de ![$ [0,1]$](img929.gif) on peut construire un élément de
on peut construire un élément de ![$ [0,1]$](img929.gif) qui n'est pas dans
qui n'est pas dans 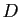 .
.
Soit
 une suite de nombres réels contenus dans
l'intervalle
une suite de nombres réels contenus dans
l'intervalle ![$ [0,1]$](img929.gif) . Chaque terme de cette suite possède un
développement décimal illimité propre
. Chaque terme de cette suite possède un
développement décimal illimité propre
On construit maintenant un nombre réel y dans [0,1] en considérant le
n-ième chiffre après la virgule de 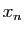 . On définit le nombre réel
. On définit le nombre réel
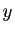 par son développement décimal propre :
par son développement décimal propre :
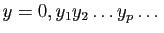 où si la n-ième décimale de
où si la n-ième décimale de 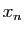 est différente de 1, alors
est différente de 1, alors 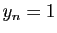 ,
sinon
,
sinon 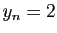 .
Le nombre
.
Le nombre 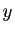 est clairement dans l'intervalle [0, 1] mais ne peut pas
apparaître dans la suite
est clairement dans l'intervalle [0, 1] mais ne peut pas
apparaître dans la suite
 , car il ne peut être égal à
aucun des
, car il ne peut être égal à
aucun des 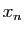 puisque pour tout
puisque pour tout 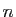 sa n-ième décimale est
différente de la n-ième décimale de
sa n-ième décimale est
différente de la n-ième décimale de 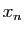 .
. 
Définitions axiomatiques de
 Le corps
Le corps
 contenant
contenant
 que nous avons construit est un
corps commutatif archimédien et complet.
Nous allons montrer qu'un tel corps
est unique à isomorphisme près.
que nous avons construit est un
corps commutatif archimédien et complet.
Nous allons montrer qu'un tel corps
est unique à isomorphisme près.
Notons que si  est un corps commutatif totalement ordonné on peut
définir, comme nous l'avons fait pour le corps
est un corps commutatif totalement ordonné on peut
définir, comme nous l'avons fait pour le corps
 , les notions de
suites convergentes et de suites de Cauchy et que les propriétés 1) à
6) restent encore valables.
, les notions de
suites convergentes et de suites de Cauchy et que les propriétés 1) à
6) restent encore valables.
Théorème 6
Si  est un corps commutatif archimédien et complet, alors il existe
un isomorphisme de
est un corps commutatif archimédien et complet, alors il existe
un isomorphisme de
 sur
sur  prolongeant l'identité de
prolongeant l'identité de
 (quand on identifie
(quand on identifie
 au sous-corps de
au sous-corps de  formé des éléments
formé des éléments
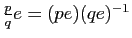 , où
, où 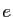 est l'élément unité de
est l'élément unité de  ).
).
Démonstration : Définissons une application
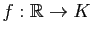 par : si
par : si
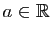 est la
classe d'une suite de Cauchy de rationnels
est la
classe d'une suite de Cauchy de rationnels
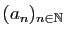 alors, on
pose,
alors, on
pose,
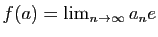 (cette limite existe puisque
(cette limite existe puisque  est complet et ne dépend pas du choix du représentant
est complet et ne dépend pas du choix du représentant
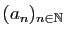 ). Par construction,
). Par construction, 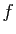 est un morphisme d'anneau
strictement croissant. Enfin,
est un morphisme d'anneau
strictement croissant. Enfin, 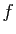 est surjective, grâce au fait que
est surjective, grâce au fait que
 est archimédien : pour tout
est archimédien : pour tout 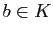 ,
,
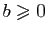 et tout entier
et tout entier 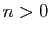 , il existe un rationnel
, il existe un rationnel 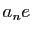 compris entre
compris entre 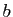 et
et 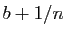 et
et
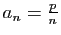 , où
, où 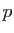 est le plus petit entier majorant
est le plus petit entier majorant
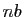 . Une telle suite
. Une telle suite
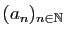 est de Cauchy, et sa classe
est de Cauchy, et sa classe
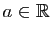 est un antécédent de
est un antécédent de 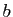 par
par 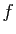 .
. 
L'unicité à isomorphisme près de
 a plusieurs conséquences. D'une
part
a plusieurs conséquences. D'une
part
 est indépendant du choix de son mode de construction, nous
avons privilégié ici une construction à partir des suites de Cauchy
(c'est une méthode classique que l'on retrouve en topologie pour
construire le complété d'un espace vectoriel topologique), d'autres
constructions sont possibles à l'aide des coupures de Dedekind ou à
l'aide des développements décimaux. D'autre part cela permet de donner
une définition axiomatique de
est indépendant du choix de son mode de construction, nous
avons privilégié ici une construction à partir des suites de Cauchy
(c'est une méthode classique que l'on retrouve en topologie pour
construire le complété d'un espace vectoriel topologique), d'autres
constructions sont possibles à l'aide des coupures de Dedekind ou à
l'aide des développements décimaux. D'autre part cela permet de donner
une définition axiomatique de
 comme étant le seul corps
commutatif archimédien et complet.
comme étant le seul corps
commutatif archimédien et complet.
Prouvons pour terminer que
 est le seul corps commutatif
totalement ordonné tel que toute partie non vide
majorée admet une borne supérieure, ce qui donne une autre
définition axiomatique de
est le seul corps commutatif
totalement ordonné tel que toute partie non vide
majorée admet une borne supérieure, ce qui donne une autre
définition axiomatique de
 .
.
Proposition 25
Soit  un corps commutatif totalement ordonné tel
que toute partie non vide majorée admet une borne supérieure, alors
un corps commutatif totalement ordonné tel
que toute partie non vide majorée admet une borne supérieure, alors
 est archimédien et complet.
est archimédien et complet.
Démonstration : Prouvons que  est archimédien.
Soient
est archimédien.
Soient 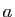 ,
, 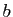 deux éléments de
deux éléments de  , on suppose
, on suppose 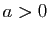 . On cherche un
entier
. On cherche un
entier 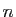 tel que
tel que 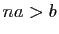 . Si
. Si
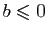 ,
, 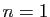 convient. Si
convient. Si 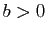 , on
considère l'ensemble
, on
considère l'ensemble
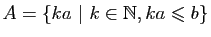 . Cet ensemble
est non vide (il contient 0) et majoré par
. Cet ensemble
est non vide (il contient 0) et majoré par 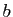 , donc il possède une
borne supérieure
, donc il possède une
borne supérieure 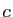 . L'élément
. L'élément 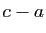 est strictement inférieur à
est strictement inférieur à 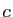 ,
par conséquent ce n'est pas un majorant de
,
par conséquent ce n'est pas un majorant de 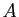 . Il existe donc un
élément
. Il existe donc un
élément 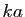 de
de 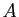 tel que
tel que 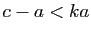 . Mais
. Mais 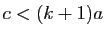 donc
donc 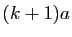 n'appartient pas à
n'appartient pas à 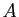 , si bien que
, si bien que 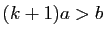 .
.
Montrons maintenant que  est complet.
Soit
est complet.
Soit
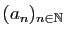 , une suite de Cauchy dans
, une suite de Cauchy dans  , nous devons
prouver que
, nous devons
prouver que
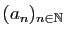 converge. La suite
converge. La suite
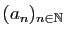 est
bornée, il existe donc un élément
est
bornée, il existe donc un élément 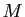 de
de  tel que pour tout entier
tel que pour tout entier
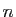 ,
,
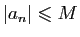 .
.
Pour tout 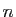 , l'ensemble
, l'ensemble
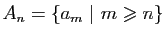 est majoré par
est majoré par
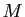 et non vide, il possède donc une borne supérieure
et non vide, il possède donc une borne supérieure 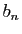 . La suite
. La suite
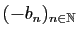 est alors croissante et majorée par
est alors croissante et majorée par 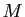 . Soit
. Soit
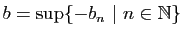 . Par définition de la borne supérieure,
pour tout
. Par définition de la borne supérieure,
pour tout
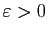 ,
,
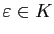 , il existe
, il existe 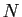 tel que
tel que
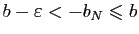 et, puisque la suite
et, puisque la suite
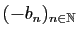 est
croissante, pour tout
est
croissante, pour tout 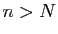 on a
on a
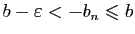 , soit
, soit
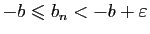 et la suite
et la suite
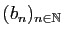 converge
donc vers
converge
donc vers 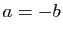 .
.
La suite
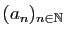 étant de Cauchy
pour tout
étant de Cauchy
pour tout
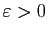 dans
dans  , il existe
, il existe
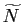 tel que pour
tous
tel que pour
tous
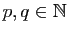
Posons
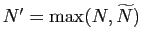 .
Pour tout
.
Pour tout
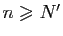 ,
,
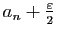 est alors un
majorant de
est alors un
majorant de 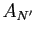 , donc un majorant de
, donc un majorant de 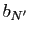 , si bien
que
, si bien
que
Ce qui montre que la suite
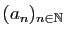 converge vers
converge vers 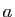 .
.
Pour prouver la réciproque de la Proposition 25, nous allons
introduire la notion d'ensembles adjacents dans un corps commutatif
 totalement ordonné.
totalement ordonné.
Lemme 7
Si le corps  est archimédien et complet et si
est archimédien et complet et si 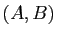 est un couple
d'ensembles adjacents de
est un couple
d'ensembles adjacents de  , il existe un unique élément
, il existe un unique élément 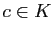 tel
que pour tout
tel
que pour tout
 ,
,
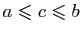 .
.
Démonstration : Par définition des ensembles adjacents, pour tout
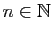 , il existe
, il existe
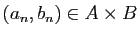 tel que
tel que
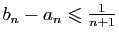 Nous allons prouver que la suite
Nous allons prouver que la suite
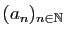 est une suite de
Cauchy dans
est une suite de
Cauchy dans  .
.
Grâce au (i) de la définition des ensembles adjacents on a
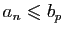 pour tous
pour tous
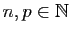 , par conséquent
, par conséquent
et donc
Soit
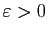 ,
,
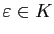 , le corps
, le corps  étant
archimédien, il existe
étant
archimédien, il existe
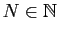 tel que
tel que
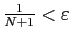 . Alors pour
. Alors pour 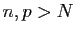 on a
on a
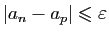 et la suite
et la suite
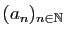 est de Cauchy
dans
est de Cauchy
dans  .
Puisque
.
Puisque  est complet, elle converge vers une limite
est complet, elle converge vers une limite 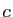 .
.
De plus par définition de 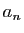 et
et 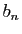 , la suite
, la suite
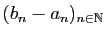 converge vers 0. On en déduit que
la suite
converge vers 0. On en déduit que
la suite
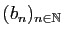 converge également vers
converge également vers 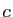 . Par ailleurs,
si
. Par ailleurs,
si 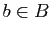 , on a, pour tout
, on a, pour tout
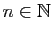 ,
,
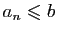 et par passage à
la limite
et par passage à
la limite
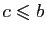 . De manière analogue on a
. De manière analogue on a
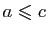 pour tout
pour tout
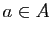 .
.
Vérifions maintenant que 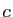 est unique. Supposons qu'il existe
est unique. Supposons qu'il existe 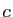 et
et
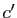 tels que pour tout
tels que pour tout
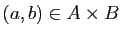
Alors pour tout
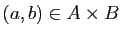 , on a
, on a
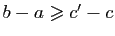 , ce qui
contredit la propriété (ii) de la définition des ensembles adjacents.
, ce qui
contredit la propriété (ii) de la définition des ensembles adjacents. 
Proposition 26
Soit  un corps commutatif archimédien et complet contenant
un corps commutatif archimédien et complet contenant
 ,
alors
,
alors  est totalement ordonné et toute partie non vide majorée de
est totalement ordonné et toute partie non vide majorée de
 admet une borne supérieure.
admet une borne supérieure.
Démonstration : Soit  une partie non vide majorée de
une partie non vide majorée de  , notons
, notons  l'ensemble des
majorants de
l'ensemble des
majorants de 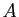 . Nous allons prouver que
. Nous allons prouver que 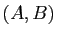 est un couple
d'ensembles adjacents de
est un couple
d'ensembles adjacents de  . Remarquons tout d'abord que
. Remarquons tout d'abord que 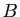 est non
vide (puisque
est non
vide (puisque 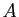 est majorée) et pour tout
est majorée) et pour tout
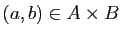 ,
,
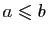 . Soit
. Soit
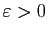 ,
,
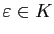 . Fixons
. Fixons 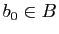 et posons
et posons
L'ensemble 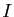 n'est pas vide car
n'est pas vide car 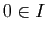 et il est majoré. En effet
soit
et il est majoré. En effet
soit 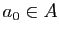 (
(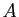 est non vide), pour tout
est non vide), pour tout 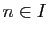 on a
on a
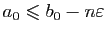 et donc
et donc
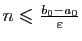 . L'ensemble
. L'ensemble 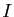 possède donc un
plus grand élément
possède donc un
plus grand élément 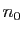 . Posons
. Posons
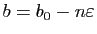 , alors
, alors 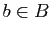 et
et
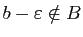 , il existe donc
, il existe donc 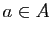 tel que
tel que
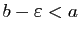 , soit
, soit
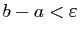 . Le couple
. Le couple 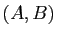 est donc
adjacent.
est donc
adjacent.
D'après le lemme 7, il existe 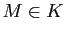 tel que pour tout
tel que pour tout
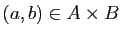 ,
,
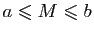 .
. 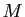 est alors le plus petit
majorant de
est alors le plus petit
majorant de 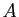 donc sa borne supérieure.
donc sa borne supérieure. 
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
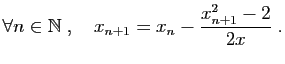
![]() totalement ordonné
contenant
totalement ordonné
contenant
![]() et dans lequel toutes les suites qui devraient
naturellement converger (ce seront les suites de Cauchy) seront
effectivement convergentes.
et dans lequel toutes les suites qui devraient
naturellement converger (ce seront les suites de Cauchy) seront
effectivement convergentes.
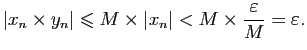
![]() et
et
![]() deux suites de
Cauchy, alors pour
deux suites de
Cauchy, alors pour
![]() ,
,
![]() , il existe
, il existe
![]() et
et
![]() tels que pour tout
tels que pour tout
![]()
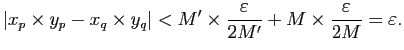
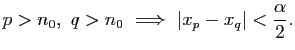
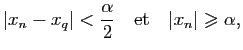
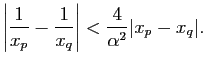
![]() , il existe des suites de Cauchy non
convergentes. Nous en avons vu des exemples plus haut. En voici un
autre.
Considérons la suite
, il existe des suites de Cauchy non
convergentes. Nous en avons vu des exemples plus haut. En voici un
autre.
Considérons la suite
![]() définie par
définie par
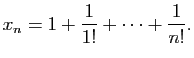
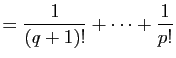
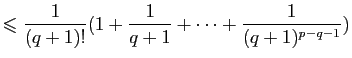
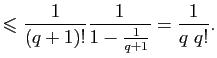
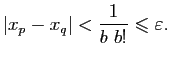
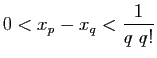
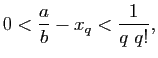
![]() définie par
définie par
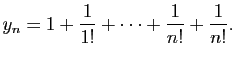
![]() est clairement croissante et la suite
est clairement croissante et la suite
![]() est décroissante
puisque
est décroissante
puisque 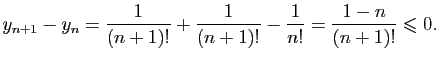
![]() en un nouvel ensemble ordonné de
nombres dans lequel toute suite de Cauchy serait convergente. Les deux
suites
en un nouvel ensemble ordonné de
nombres dans lequel toute suite de Cauchy serait convergente. Les deux
suites
![]() et
et
![]() précédentes auraient
alors une limite commune dans cet ensemble qui serait située entre
chacun des nombres rationnels
précédentes auraient
alors une limite commune dans cet ensemble qui serait située entre
chacun des nombres rationnels ![]() et
et ![]() .
Nous allons construire un tel ensemble.
.
Nous allons construire un tel ensemble.
![]() contenant
contenant
![]() et qui sera archimédien et complet comme quotient de l'ensemble des
suites de Cauchy de
et qui sera archimédien et complet comme quotient de l'ensemble des
suites de Cauchy de
![]() .
.
![]() l'ensemble des suites de rationnels, c'est-à-dire
l'ensemble des applications de
l'ensemble des suites de rationnels, c'est-à-dire
l'ensemble des applications de
![]() dans
dans
![]() , et
, et
![]() le
sous-ensemble de
le
sous-ensemble de
![]() constitué des suites de Cauchy.
constitué des suites de Cauchy.
![]() des
suites de Cauchy dans
des
suites de Cauchy dans
![]() est muni d'une structure d'anneau
commutatif si on pose pour
est muni d'une structure d'anneau
commutatif si on pose pour
![]() et
et
![]()
![]() Soit
Soit
![]() une suite de Cauchy de rationnels, on dira que
une suite de Cauchy de rationnels, on dira que
![]() si et seulement si
si et seulement si
![]() , alors
, alors
![]() équivaut à
équivaut à
![]() , le cas où
, le cas où
![]() se traite de manière analogue. Si
se traite de manière analogue. Si
![]() et si
et si
![]() ,
,
![]() est donné, il existe
est donné, il existe ![]() tel
que
tel
que
![]() si
si ![]() . Comme
. Comme
![]() , il
existe
, il
existe ![]() tel que si
tel que si ![]() alors
alors
![]() . Ainsi pour
. Ainsi pour
![]() on a
on a
![]() , c'est-à-dire
, c'est-à-dire
![]() .
. ![]()
![]() et
et
![]() .
. ![]() en posant
en posant
![]() si et seulement si
si et seulement si
![]() . Grâce aux propriétés (i), (ii) et (iii) du Lemme
3,
. Grâce aux propriétés (i), (ii) et (iii) du Lemme
3,
![]() est un corps totalement
ordonné. Notons que l'injection
est un corps totalement
ordonné. Notons que l'injection ![]() de
de
![]() dans
dans
![]() est
croissante, puisque
est
croissante, puisque
![]() dans
dans
![]() équivaut à
équivaut à
![]() .
.
![]() Les définitions sont analogues à celles des suites de Cauchy et des
suites convergentes dans
Les définitions sont analogues à celles des suites de Cauchy et des
suites convergentes dans
![]() , mais cette fois on autorise
, mais cette fois on autorise
![]() à appartenir à
à appartenir à
![]() . Comme
. Comme
![]() est archimédien cela
n'apporte rien car si
est archimédien cela
n'apporte rien car si
![]() est un nombre réel, il existe
est un nombre réel, il existe
![]() tel que
tel que
![]() (il suffit
de poser
(il suffit
de poser
![]() , avec
, avec
![]() ).
).
![]() est complet nous avons besoin de quelques
lemmes qui ont un intérêt intrinsèque.
est complet nous avons besoin de quelques
lemmes qui ont un intérêt intrinsèque.
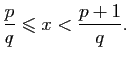
![]()
![]() , il résulte du Lemme 4 qu'il existe
, il résulte du Lemme 4 qu'il existe
![]() tel que
tel que
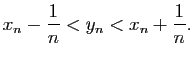
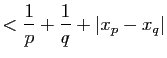
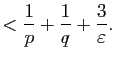
![]()
![]() si
si
![]() , d'où
, d'où
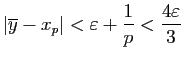
![]() , l'entier
, l'entier ![]() du Lemme 6
s'appelle la partie entière de
du Lemme 6
s'appelle la partie entière de ![]() et est habituellement
noté
et est habituellement
noté
![]() . On appelle partie décimale
de
. On appelle partie décimale
de ![]() la différence
la différence
![]() . On la note
. On la note ![]() ,
elle appartient à l'intervalle
,
elle appartient à l'intervalle ![]() .
.
![]() ,
,
![]() , prenons
, prenons
![]() . Si
. Si
![]() , d'après le Lemme 6, il existe un unique
, d'après le Lemme 6, il existe un unique
![]() tel que
tel que
![]() par
par ![]() , on obtient
, on obtient ![]() qui vérifie
qui vérifie
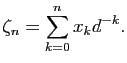
![]() ,
,
![]() par la
formule du binôme de Newton donc
par la
formule du binôme de Newton donc
![]() . La
suite
. La
suite
![]() des valeurs approchées vérifie
des valeurs approchées vérifie
![]() et converge donc vers
et converge donc vers ![]() quand
quand ![]() tend vers
l'infini.
tend vers
l'infini.
![]() la suite
la suite
![]() s'appelle un
développement décimal illimité de
s'appelle un
développement décimal illimité de ![]() et on écrit
et on écrit
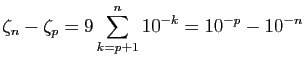
![]() possède un unique
développement décimal illimité propre. Si on note
possède un unique
développement décimal illimité propre. Si on note
![]() l'ensemble
des suites
l'ensemble
des suites
![]() d'entiers relatifs telles que pour tout
d'entiers relatifs telles que pour tout
![]() ,
,
![]() et pour tout
et pour tout
![]() il
existe
il
existe
![]() tel que
tel que ![]() , nous avons donc défini une application
, nous avons donc défini une application
![]() qui a chaque nombre réel
qui a chaque nombre réel ![]() associe son
développement décimal illimité propre.
associe son
développement décimal illimité propre.
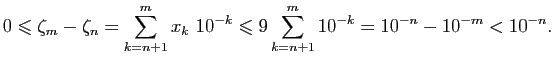
![]() l'application de
l'application de
![]() dans
dans
![]() qui à la suite
qui à la suite
![]() associe le nombre réel
associe le nombre réel ![]() défini par la suite
défini par la suite
![]() , il est clair que
, il est clair que
![]() et
et
![]() sont respectivement l'application identique de
sont respectivement l'application identique de
![]() et celle de
et celle de
![]() , ce qui prouve que
, ce qui prouve que ![]() est bijective et
que
est bijective et
que
![]() .
. ![]()
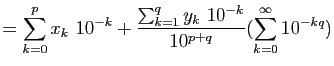
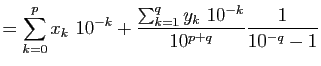
![]() avec
avec ![]() et
et ![]() des entiers
premiers entre eux. On définit par récurrence une suite d'entiers
des entiers
premiers entre eux. On définit par récurrence une suite d'entiers
![]() ,
,
![]() , tels que
, tels que
![]() en considérant
les restes des
divisions euclidiennes successives de
en considérant
les restes des
divisions euclidiennes successives de ![]() par
par ![]() , puis de
, puis de ![]() par
par ![]() et ainsi de suite. En notant
et ainsi de suite. En notant ![]() les différents
quotients on aura
les différents
quotients on aura
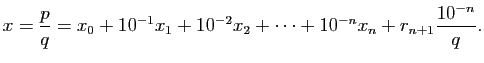
![]() est le développement décimal de
est le développement décimal de ![]() car
car
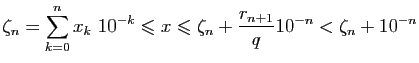
![]() , qui
contient
, qui
contient
![]() , est en fait beaucoup plus gros que
, est en fait beaucoup plus gros que
![]() .
.
![]() une suite de nombres réels contenus dans
l'intervalle
une suite de nombres réels contenus dans
l'intervalle ![]() . Chaque terme de cette suite possède un
développement décimal illimité propre
. Chaque terme de cette suite possède un
développement décimal illimité propre ![]() . On définit le nombre réel
. On définit le nombre réel
![]() par son développement décimal propre :
par son développement décimal propre :
![]() où si la n-ième décimale de
où si la n-ième décimale de ![]() est différente de 1, alors
est différente de 1, alors ![]() ,
sinon
,
sinon ![]() .
Le nombre
.
Le nombre ![]() est clairement dans l'intervalle [0, 1] mais ne peut pas
apparaître dans la suite
est clairement dans l'intervalle [0, 1] mais ne peut pas
apparaître dans la suite
![]() , car il ne peut être égal à
aucun des
, car il ne peut être égal à
aucun des ![]() puisque pour tout
puisque pour tout ![]() sa n-ième décimale est
différente de la n-ième décimale de
sa n-ième décimale est
différente de la n-ième décimale de ![]() .
. ![]()
![]() Le corps
Le corps
![]() contenant
contenant
![]() que nous avons construit est un
corps commutatif archimédien et complet.
Nous allons montrer qu'un tel corps
est unique à isomorphisme près.
que nous avons construit est un
corps commutatif archimédien et complet.
Nous allons montrer qu'un tel corps
est unique à isomorphisme près.
![]() est un corps commutatif totalement ordonné on peut
définir, comme nous l'avons fait pour le corps
est un corps commutatif totalement ordonné on peut
définir, comme nous l'avons fait pour le corps
![]() , les notions de
suites convergentes et de suites de Cauchy et que les propriétés 1) à
6) restent encore valables.
, les notions de
suites convergentes et de suites de Cauchy et que les propriétés 1) à
6) restent encore valables.
![]() a plusieurs conséquences. D'une
part
a plusieurs conséquences. D'une
part
![]() est indépendant du choix de son mode de construction, nous
avons privilégié ici une construction à partir des suites de Cauchy
(c'est une méthode classique que l'on retrouve en topologie pour
construire le complété d'un espace vectoriel topologique), d'autres
constructions sont possibles à l'aide des coupures de Dedekind ou à
l'aide des développements décimaux. D'autre part cela permet de donner
une définition axiomatique de
est indépendant du choix de son mode de construction, nous
avons privilégié ici une construction à partir des suites de Cauchy
(c'est une méthode classique que l'on retrouve en topologie pour
construire le complété d'un espace vectoriel topologique), d'autres
constructions sont possibles à l'aide des coupures de Dedekind ou à
l'aide des développements décimaux. D'autre part cela permet de donner
une définition axiomatique de
![]() comme étant le seul corps
commutatif archimédien et complet.
comme étant le seul corps
commutatif archimédien et complet.
![]() est le seul corps commutatif
totalement ordonné tel que toute partie non vide
majorée admet une borne supérieure, ce qui donne une autre
définition axiomatique de
est le seul corps commutatif
totalement ordonné tel que toute partie non vide
majorée admet une borne supérieure, ce qui donne une autre
définition axiomatique de
![]() .
.
![]() est complet.
Soit
est complet.
Soit
![]() , une suite de Cauchy dans
, une suite de Cauchy dans ![]() , nous devons
prouver que
, nous devons
prouver que
![]() converge. La suite
converge. La suite
![]() est
bornée, il existe donc un élément
est
bornée, il existe donc un élément ![]() de
de ![]() tel que pour tout entier
tel que pour tout entier
![]() ,
,
![]() .
.
![]() , l'ensemble
, l'ensemble
![]() est majoré par
est majoré par
![]() et non vide, il possède donc une borne supérieure
et non vide, il possède donc une borne supérieure ![]() . La suite
. La suite
![]() est alors croissante et majorée par
est alors croissante et majorée par ![]() . Soit
. Soit
![]() . Par définition de la borne supérieure,
pour tout
. Par définition de la borne supérieure,
pour tout
![]() ,
,
![]() , il existe
, il existe ![]() tel que
tel que
![]() et, puisque la suite
et, puisque la suite
![]() est
croissante, pour tout
est
croissante, pour tout ![]() on a
on a
![]() , soit
, soit
![]() et la suite
et la suite
![]() converge
donc vers
converge
donc vers ![]() .
.
![]() étant de Cauchy
pour tout
étant de Cauchy
pour tout
![]() dans
dans ![]() , il existe
, il existe
![]() tel que pour
tous
tel que pour
tous
![]()
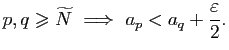
![]() totalement ordonné.
totalement ordonné.
![]() ,
,
![]() ;
;
![]() ,
,
![]() , il existe
, il existe
![]() tel que
tel que
![]() .
. ![]() pour tous
pour tous
![]() , par conséquent
, par conséquent
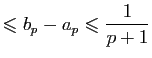
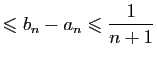
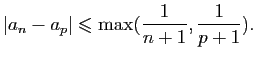
![]() ,
,
![]() , le corps
, le corps ![]() étant
archimédien, il existe
étant
archimédien, il existe
![]() tel que
tel que
![]() . Alors pour
. Alors pour ![]() on a
on a
![]() et la suite
et la suite
![]() est de Cauchy
dans
est de Cauchy
dans ![]() .
Puisque
.
Puisque ![]() est complet, elle converge vers une limite
est complet, elle converge vers une limite ![]() .
.
![]() et
et ![]() , la suite
, la suite
![]() converge vers 0. On en déduit que
la suite
converge vers 0. On en déduit que
la suite
![]() converge également vers
converge également vers ![]() . Par ailleurs,
si
. Par ailleurs,
si ![]() , on a, pour tout
, on a, pour tout
![]() ,
,
![]() et par passage à
la limite
et par passage à
la limite
![]() . De manière analogue on a
. De manière analogue on a
![]() pour tout
pour tout
![]() .
.
![]() est unique. Supposons qu'il existe
est unique. Supposons qu'il existe ![]() et
et
![]() tels que pour tout
tels que pour tout
![]()
![]() tel que pour tout
tel que pour tout
![]() ,
,
![]() .
. ![]() est alors le plus petit
majorant de
est alors le plus petit
majorant de ![]() donc sa borne supérieure.
donc sa borne supérieure. ![]()
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales