Construction des rationnels

Il reste dans $\mathbb{Z}$ des équations sans solution, comme $a=b\times x$ pour $b\neq 0$, dont la solution en $x$ devrait être le produit de $a$ par un inverse de $b$ pour la multiplication. Or dans $\mathbb{Z}\setminus\{0\}$ seuls $+1$ et $-1$ ont un inverse. L'idée est alors de reproduire pour la multiplication dans $\mathbb{Z}\setminus\{0\}$ la procédure utilisée pour l'addition dans $\mathbb{N}$ afin de construire un groupe multiplicatif $\mathbb{Q}^*$ contenant $\mathbb{Z}\setminus\{0\}$. La structure d'anneau de $\mathbb{Z}$ sera alors prolongée à ce nouvel ensemble, faisant de $(\mathbb{Q},+,\times)$ un corps.

Dans l'ensemble $\mathbb{Z}^*=\mathbb{Z}\setminus\{0\}$ la loi de composition interne $\times$ possède les mêmes propriétés que l'addition dans $\mathbb{N}$, on peut donc appliquer la même procédure que dans la section 1.3 pour construire un nouvel ensemble de nombres noté $\mathbb{Q}$ contenant $\mathbb{Z}$ et tel que $\mathbb{Q}\setminus\{0\}$ possède une structure de groupe multiplicatif.

Considérons sur $\mathbb{Z}^*\times\mathbb{Z}^*$, la relation $\mathcal{R}$ définie par

$$(a,b)\mathcal{R} (a',b')\;\Longleftrightarrow\; a\times b'=a'\times b.$$ (7)

C'est une relation d'équivalence compatible avec la multiplication sur $\mathbb{Z}^*\times\mathbb{Z}^*$. La démonstration de cette assertion est analogue à celle de la Proposition 11 .

On notera $\frac{a}{b}$ la classe du couple $(a,b)$ pour la relation $\mathcal{R}$. On remarquera que pour tout $c\in\mathbb{Z}^*$, on a $\frac{a}{b}=\frac{a\times c}{b\times c}$.

Proposition 15   L'ensemble quotient $\mathbb{Z}^*\times\mathbb{Z}^*/\mathcal{R}$ munit de la loi quotient déduite de la multiplication sur $\mathbb{Z}^*\times\mathbb{Z}^*$, notée encore $\times$, est un groupe abélien, on le note $\mathbb{Q}^*$.

L'élément neutre ce groupe est la classe du couple $(1,1)$. Un élément $(a,b)$ de $\mathbb{Z}^*\times\mathbb{Z}^*/\mathcal{R}$ appartient à $\frac{1}{1}$ si et seulement si $a\times 1=1\times b$, c'est-à-dire $a=b$. L'inverse de $\frac{a}{b}$ est $\frac{b}{a}$.

La démonstration de la proposition est analogue à celle de la Proposition 12.

Proposition 16   On définit un morphisme injectif $f : \mathbb{Z}^*\to\mathbb{Q}^*$ en posant $f(a)=\frac{a}{1}$

Démonstration : Vérifions que l'application $f : \mathbb{Z}^*\to\mathbb{Q}^*$ définie par $f(a)=\frac{a}{1}$ est multiplicative. Soient $a$ et $b$ dans $\mathbb{Z}^*$, alors

$$f(a\times b)=\frac{a\times b}{1}=\frac{a}{1}\times \frac{b}{1}=f(a)\times f(b)$$

par définition de la multiplication dans $\mathbb{Q}^*$. Montrons maintenant que $f$ est injective. Soient $a$ et $b$ dans $\mathbb{Z}^*$ tels que $f(a)=f(b)$, c'est-à-dire $\frac{a}{1}=\frac{b}{1}$. Par définition de la relation $\mathcal{R}$ cela signifie que $a\times 1=b\times 1$, soit $a=b$, d'où l'injectivité de l'application $f$. $\square$

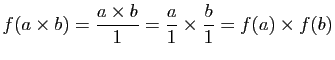
Pour simplifier les écritures, on notera $a$ à la place de $\frac{a}{1}$ l'élément $f(a)$ si $a\in\mathbb{Z}^*$. On écrira souvent $ab$ à la place de $a\times b$ pour le produit de deux éléments de $\mathbb{Z}^*$.

En raison de la structure de groupe multiplicatif de $\mathbb{Q}^*$, si $a\in\mathbb{Z}^*$ et $b\in\mathbb{Z}^*$, l'équation $a=b\times x$ possède toujours une unique solution : l'élément $\frac{a}{b}$ de $\mathbb{Q}^*$. De plus si $a=0$ et $b\in\mathbb{Z}^*$, l'élément 0 de $\mathbb{Z}$ est l'unique solution de $a=b\times x$, car $\mathbb{Z}$ est un anneau intègre.

Définition 6   On appelle ensemble des nombres rationnels l'ensemble $\mathbb{Q}^*$ auquel on a ajouté l'élément 0 de $\mathbb{Z}$. On le note $\mathbb{Q}$.

Pour compléter la structure algébrique de $\mathbb{Q}$ nous allons prolonger à $\mathbb{Q}$ la structure de groupe additif de $\mathbb{Z}$. Soient $x=\frac{a}{b}$ et $y=\frac{c}{d}$ deux éléments de $\mathbb{Q}$, on pose

$$x+y=\frac{ad+bc}{bd}.$$

Vérifions que cette définition a bien un sens en remarquant qu'elle est indépendante des représentants choisis. Nous devons prouver que si $(a,b)\mathcal{R} (a',b')$ et $(c,d)\mathcal{R} (c',d')$ alors $(ad+bc,bd)\mathcal{R}(a'd'+b'c',b'd')$. Supposons que $ab'=a'b$ et $cd'=c'd$, alors

$$(ad+bc)b'd' =(ab')dd'+(cd')bb'$$

$$=(a'b)dd'+(c'd)bb'$$

$$=(a'd'+c'd')bd,$$

c'est-à-dire $(ad+bc,bd)\mathcal{R}(a'd'+b'c',b'd')$.

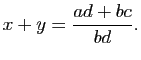
Par un calcul direct, il résulte immédiatement des propriétés de l'addition et de la multiplication dans $\mathbb{Z}$ que l'addition est associative, commutative et que la multiplication est distributive par rapport à l'addition. Notons que $0=\frac{0}{1}$ vérifie :

$$\frac{a}{b}+0=0+\frac{a}{b}=\frac{a\times 1+0\times b}{b\times 1}=\frac{a}{b}\;,$$

c'est donc un élément neutre pour l'addition. De plus si $x=\frac{a}{b}$, posons $-x=\frac{-a}{b}=(-1)\times x$, alors

$$x+(-x)=\frac{ab+(-a)b}{bb}=\frac{ab-ab}{bb}=\frac{0}{bb}=0\;.$$

Tout élément $x$ de $\mathbb{Q}$ possède un inverse pour l'addition et $(\mathbb{Q},+)$ est donc un groupe abélien.

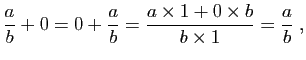
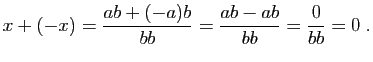
L'ensemble $\mathbb{Q}$ ainsi construit muni des lois $+$ et $\times$ possède une structure de corps.

Si $x$ et $y$ sont dans $\mathbb{Z}$, on identifie $x$ avec $\frac{x}{1}$ et $y$ avec $\frac{y}{1}$, alors

$$x+y=\frac{x\times 1+1\times y}{1\times 1}=\frac{x+y}{1}\;,$$

après identification. La loi $+$ prolonge donc l'addition sur $\mathbb{Z}$ et $(\mathbb{Z},+,\times)$ est un sous anneau de $\mathbb{Q}$.

Proposition 17   L'ensemble $\mathbb{Q}$ est dénombrable.

Démonstration : L'ensemble $\mathbb{Q}$ s'injecte dans le produit cartésien $\mathbb{Z}\times\mathbb{N}$ et contient $\mathbb{N}$. Il suffit donc de prouver que $\mathbb{Z}\times\mathbb{N}$ est dénombrable, mais comme $\mathbb{Z}$ est dénombrable on est ramené à prouver que $\mathbb{N}\times\mathbb{N}$ est dénombrable. L'application $f:\mathbb{N}\times\mathbb{N}\to\mathbb{N}$ définie par

$$f(p,q)=q+\sum_{i=0}^{p+q}i=\frac{(p+q)(p+q+1)}{2}+q\;,$$

qui consiste à compter diagonalement les couples $(p,q)$ donne la bijection cherchée. $\square$

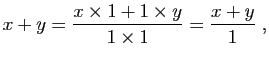
Relation d'ordre dans $\mathbb{Q}$

Pour terminer nous allons étendre à $\mathbb{Q}$ la relation d'ordre de $\mathbb{Z}$. Rappelons que si $x$ et $y$ sont deux éléments de $\mathbb{Z}$ alors $x\leqslant y$ si et seulement si $y-x\in\mathbb{N}$ soit $0\leqslant y-x$. Pour commencer nous allons définir la notion de nombre rationnel positif. Si $\frac{a}{b}\in\mathbb{Q}$, nous dirons que $0\leqslant \frac{a}{b}$ si et seulement si $0\leqslant a\times b$. Cette définition ne dépend pas du représentant choisi. En effet si $\frac{a}{b}=\frac{a'}{b'}$, c'est-à-dire si $a\times b'=a'\times b$, alors $(a\times b)\times (b'\times b')=(a'\times b')\times (b\times b)$ et puisque $b\times b$ et $b'\times b'$ sont tous deux positifs et non nuls comme produits de nombres entiers de même signe, $a\times b$ et $a'\times b'$ ont le même signe.

Avec cette définition, les éléments de $\mathbb{Z}$ positifs au sens de $\mathbb{Q}$ sont exactement les éléments positifs de $\mathbb{Z}$, c'est-à-dire les éléments de $\mathbb{N}$. Par analogie avec la relation d'ordre dans $\mathbb{Z}$, si $x$ et $y$ sont deux éléments de $\mathbb{Q}$, nous posons $x\leqslant y$ si et seulement si $0\leqslant y-x$. Cette relation est une relation d'ordre qui prolonge la relation d'ordre de $\mathbb{Z}$.

La relation d'ordre $\leqslant$ est compatible avec l'addition et la multiplication sur $\mathbb{Q}$ au sens suivant : soient $x$, $y$ et $z$ trois éléments de $\mathbb{Q}$

$\bullet$ si $x\leqslant y$, alors $x+z\leqslant y+z$ puisque $y-x=(y+z)-(x+z)$,

$\bullet$ si $x\leqslant y$ et $0\leqslant z$, alors $x\times z\leqslant y\times z$ puisque $(y\times z)-(x\times z)=(y-x)\times z$ et en particulier si $x=0$ on obtient que, si $0\leqslant y$ et $0\leqslant z$, alors $0\leqslant y\times z$.

On écrira de manière équivalente :

$x\leqslant y$ ou $y\geqslant x$,

$x\leqslant y, x\neq y$ ou $x< y$ ou $y>x$.

Dans la suite nous utiliserons la notation suivante : si $x\in\mathbb{Q}$, on pose $\vert x\vert=\max(x,-x)$. On a bien sûr $\vert x\vert=x$, si $x\geqslant 0$, et $\vert x\vert=-x$, si $x\leqslant 0$.