Comme vous l'avez vu pour le codage RSA, la cryptographie est grande consommatrice de nombres premiers, les plus
imposants possibles évidemment. Un moyen de trouver de grands nombres premiers est de les chercher parmi les nombres dits
«de Mersenne», autrement dit sous la forme 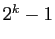 . Pourquoi ? Parce qu'il existe un test de primalité extrêmement
simple pour de tels nombres : le test de Lucas-Lehmer. Considérons la suite définie par
. Pourquoi ? Parce qu'il existe un test de primalité extrêmement
simple pour de tels nombres : le test de Lucas-Lehmer. Considérons la suite définie par 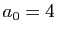 et pour
et pour 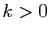 ,
,
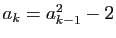 . Il se trouve que pour
. Il se trouve que pour 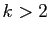 , le nombre
, le nombre 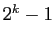 est premier si et seulement si il divise
est premier si et seulement si il divise 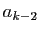 . Essayez pour les premiers termes :
. Essayez pour les premiers termes :
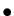
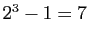 divise
divise 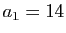
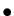
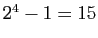 ne divise pas
ne divise pas 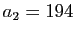
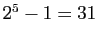 divise
divise 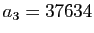
... étonnant non ? Avec un peu d'astuce, le test peut être implémenté en
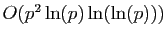 opérations pour un
nombre de
opérations pour un
nombre de 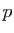 bits, ce qui est bien plus rapide que tous les algorithmes généraux connus.
Un gigantesque effort collaboratif de calcul distribué (Great Internet Mersenne Prime Search)
vise à trouver des nombres de Mersenne premiers les plus grands possibles.
Le plus grand connu à ce jour est
bits, ce qui est bien plus rapide que tous les algorithmes généraux connus.
Un gigantesque effort collaboratif de calcul distribué (Great Internet Mersenne Prime Search)
vise à trouver des nombres de Mersenne premiers les plus grands possibles.
Le plus grand connu à ce jour est
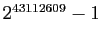 qui a plus de 12 millions de chiffres en écriture décimale.
Rien de vous empêche de participer en offrant le temps de calcul de votre ordinateur. Vous ferez progresser le calcul distribué,
mais pas la cryptographie : les nombres de Mersenne sont trop connus pour offrir un niveau de sécurité suffisant. S'il suffisait
de tester quelques nombres de Mersenne pour décomposer une clé publique en deux facteurs premiers, le code RSA perdrait
beaucoup de son intérêt.
Gauss écrivait :
qui a plus de 12 millions de chiffres en écriture décimale.
Rien de vous empêche de participer en offrant le temps de calcul de votre ordinateur. Vous ferez progresser le calcul distribué,
mais pas la cryptographie : les nombres de Mersenne sont trop connus pour offrir un niveau de sécurité suffisant. S'il suffisait
de tester quelques nombres de Mersenne pour décomposer une clé publique en deux facteurs premiers, le code RSA perdrait
beaucoup de son intérêt.
Gauss écrivait :
Le problème de distinguer les nombres premiers des nombres composés, et de décomposer ces derniers en facteurs premiers
est connu pour être un des plus importants et des plus utiles en arithmétique. Il a engagé l'industrie et la sagesse des géomètres
anciens et modernes à un tel point que la dignité de la science elle-même requiert que tous les moyens possibles
soient explorés pour la résolution d'un problème si important et si célèbre.
La véritable difficulté est de tester des nombres quelconques, et donc de disposer d'un algorithme
permettant de décider de façon certaine si un nombre est premier ou non.
Ératosthène (276-194 av. J.C.) savait déjà comment énumérer tous les nombres premiers inférieurs
à un nombre 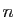 donné. L'algorithme, qui porte le nom de «Crible d'Ératosthène», est bien connu :
donné. L'algorithme, qui porte le nom de «Crible d'Ératosthène», est bien connu :
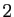 est le plus petit nombre premier. On peut éliminer
tous les multiples de
est le plus petit nombre premier. On peut éliminer
tous les multiples de 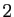 . On itère ensuite en conservant le plus
petit entier qui n'a pas encore été
éliminé et en éliminant tous ses multiples.
Mais pour décider si
. On itère ensuite en conservant le plus
petit entier qui n'a pas encore été
éliminé et en éliminant tous ses multiples.
Mais pour décider si 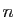 est premier en utilisant cet algorithme, le
nombre d'opérations est gigantesque, beaucoup trop
grand pour la pratique. Une autre manière de tester la primalité est d'utiliser le théorème de
Wilson :
est premier en utilisant cet algorithme, le
nombre d'opérations est gigantesque, beaucoup trop
grand pour la pratique. Une autre manière de tester la primalité est d'utiliser le théorème de
Wilson : 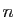 est premier si et seulement si
est premier si et seulement si
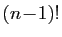 est congru à
est congru à
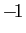 modulo
modulo 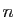 . Cela requiert de l'ordre de
. Cela requiert de l'ordre de 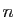 multiplications
modulo
multiplications
modulo 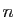 , ce qui est encore beaucoup trop lent.
, ce qui est encore beaucoup trop lent.
Quand en 2002 Agrawal, Kayal et Saxena ont annoncé «PRIMES is in
P», la nouvelle a fait sensation.
Enfin un test de primalité, dont on peut démontrer qu'il décide
de façon certaine si 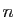 est premier,
en un nombre d'opérations polynomial en
est premier,
en un nombre d'opérations polynomial en 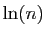 .
L'article original était théorique, mais très vite
des implémentations ont suivi, avec des raffinements et des
améliorations. Les algorithmes AKS sont maintenant toute une famille
et sont
couramment utilisés. Deux points méritent d'être soulignés dans cette histoire.
Le premier est que l'algorithme utilise un résultat d'arithmétique vieux de deux siècles
élaboré dans la quête du Dernier Théorème de Fermat,
précisément celui qui porte le nom de Sophie Germain.
L'autre est que Neeraj Kayal et Nitin Saxena, à l'époque de leur
découverte, étaient deux étudiants en Btech (équivalent d'un
Master Professionnel) d'Informatique à l'Indian Institute of Technology de Kampur,
effectuant leur mémoire sous la direction de Manindra Agrawal.
.
L'article original était théorique, mais très vite
des implémentations ont suivi, avec des raffinements et des
améliorations. Les algorithmes AKS sont maintenant toute une famille
et sont
couramment utilisés. Deux points méritent d'être soulignés dans cette histoire.
Le premier est que l'algorithme utilise un résultat d'arithmétique vieux de deux siècles
élaboré dans la quête du Dernier Théorème de Fermat,
précisément celui qui porte le nom de Sophie Germain.
L'autre est que Neeraj Kayal et Nitin Saxena, à l'époque de leur
découverte, étaient deux étudiants en Btech (équivalent d'un
Master Professionnel) d'Informatique à l'Indian Institute of Technology de Kampur,
effectuant leur mémoire sous la direction de Manindra Agrawal.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() est premier,
en un nombre d'opérations polynomial en
est premier,
en un nombre d'opérations polynomial en ![]() .
L'article original était théorique, mais très vite
des implémentations ont suivi, avec des raffinements et des
améliorations. Les algorithmes AKS sont maintenant toute une famille
et sont
couramment utilisés. Deux points méritent d'être soulignés dans cette histoire.
Le premier est que l'algorithme utilise un résultat d'arithmétique vieux de deux siècles
élaboré dans la quête du Dernier Théorème de Fermat,
précisément celui qui porte le nom de Sophie Germain.
L'autre est que Neeraj Kayal et Nitin Saxena, à l'époque de leur
découverte, étaient deux étudiants en Btech (équivalent d'un
Master Professionnel) d'Informatique à l'Indian Institute of Technology de Kampur,
effectuant leur mémoire sous la direction de Manindra Agrawal.
.
L'article original était théorique, mais très vite
des implémentations ont suivi, avec des raffinements et des
améliorations. Les algorithmes AKS sont maintenant toute une famille
et sont
couramment utilisés. Deux points méritent d'être soulignés dans cette histoire.
Le premier est que l'algorithme utilise un résultat d'arithmétique vieux de deux siècles
élaboré dans la quête du Dernier Théorème de Fermat,
précisément celui qui porte le nom de Sophie Germain.
L'autre est que Neeraj Kayal et Nitin Saxena, à l'époque de leur
découverte, étaient deux étudiants en Btech (équivalent d'un
Master Professionnel) d'Informatique à l'Indian Institute of Technology de Kampur,
effectuant leur mémoire sous la direction de Manindra Agrawal.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales