Le plus célèbre des codes à clé publique est dû à Ron Rivest, Adi Shamir et Leonard Adleman du MIT.
La clé publique est connue de tous et est utilisée pour coder les messages. Par contre un message codé
par la clé publique ne peut être décodé que par quelqu'un qui connaît la clé privée.
Les clés sont constituées de la façon suivante.
- Choisir deux (grands) nombres premiers
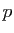 et
et 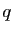 .
.
- Calculer
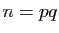 : les opérations s'effectueront modulo
: les opérations s'effectueront modulo  .
.
- Calculer
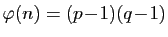 .
.
- Choisir un entier
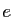 inférieur à
inférieur à
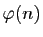 et premier avec
et premier avec
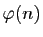 : c'est l'exposant de la clé publique.
: c'est l'exposant de la clé publique.
- Calculer l'inverse
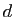 de
de 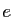 pour la multiplication modulo
pour la multiplication modulo
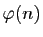 (il existe et est unique puisque
(il existe et est unique puisque 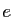 et
et 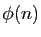 sont
premiers entre eux : calcul par l'algorithme d'Euclide).
L'entier
sont
premiers entre eux : calcul par l'algorithme d'Euclide).
L'entier 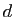 est l'exposant de la clé privée.
est l'exposant de la clé privée.
La clé publique se compose de l'entier  et de l'exposant
et de l'exposant 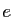 , connus de tous. La clé privée est l'exposant
, connus de tous. La clé privée est l'exposant 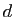 qui doit être
tenu secret. Évidemment, quelqu'un qui connaît
qui doit être
tenu secret. Évidemment, quelqu'un qui connaît  peut théoriquement
retrouver ses deux facteurs premiers
peut théoriquement
retrouver ses deux facteurs premiers 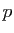 et
et 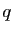 et donc calculer
et donc calculer
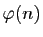 puis
puis 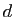 connaissant
connaissant 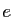 . La sécurité du système repose sur le fait que la décomposition d'un nombre
en produit de facteurs premiers est très coûteuse en temps de calcul : il est virtuellement impossible
de décomposer un nombre produit de deux très grands facteurs premiers.
Cela n'empêche pas les utilisateurs de changer assez souvent de clé par mesure de sécurité.
. La sécurité du système repose sur le fait que la décomposition d'un nombre
en produit de facteurs premiers est très coûteuse en temps de calcul : il est virtuellement impossible
de décomposer un nombre produit de deux très grands facteurs premiers.
Cela n'empêche pas les utilisateurs de changer assez souvent de clé par mesure de sécurité.
Voici comment fonctionnent le codage et le décodage.
Le message à transmettre est d'abord transformé en un entier (par exemple par concaténation des codes ascii
des caractères qui le composent). Notons 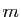 cet entier qui est censé être inférieur à
cet entier qui est censé être inférieur à  .
Le codage le transforme en
.
Le codage le transforme en 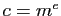 modulo
modulo  . Pour décoder, il faut connaître
. Pour décoder, il faut connaître
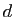 et calculer
et calculer 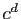 modulo
modulo  . Miracle, on retrouve
. Miracle, on retrouve 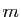 .
Vous pouvez nous croire sur parole, mais ce serait dommage, car la démonstration
est parfaitement à votre portée.
.
Vous pouvez nous croire sur parole, mais ce serait dommage, car la démonstration
est parfaitement à votre portée.
Définition 9
On appelle caractéristique d'Euler la fonction qui à un entier  fait correspondre le nombre d'entiers
premiers avec
fait correspondre le nombre d'entiers
premiers avec  , compris entre
, compris entre 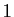 et
et  . On note cette fonction
. On note cette fonction 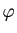 .
.
Si 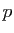 est premier, alors
est premier, alors
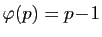 , puisque tout entier strictement inférieur à
, puisque tout entier strictement inférieur à 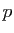 est premier avec
est premier avec 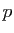 .
Si
.
Si 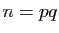 est le produit des 2 nombres premiers
est le produit des 2 nombres premiers 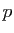 et
et 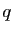 , alors
, alors
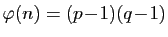 . Pourquoi ? Vous pouvez trouver tout seul :
comptez les multiples de
. Pourquoi ? Vous pouvez trouver tout seul :
comptez les multiples de 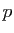 puis les multiples de
puis les multiples de 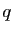 , entre
, entre 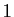 et
et 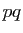 (ne comptez pas
(ne comptez pas 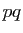 deux fois).
Voici maintenant la généralisation du petit théorème de Fermat,
que nous vous avons posé en exercice.
deux fois).
Voici maintenant la généralisation du petit théorème de Fermat,
que nous vous avons posé en exercice.
Théorème 9
Soit  un entier et
un entier et 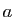 un entier premier avec
un entier premier avec  . Alors
. Alors
![$ a^{\varphi(n)}\equiv 1\;[n]$](img909.gif) .
.
Cela aussi, vous pouvez le démontrer vous-mêmes : considérez
le sous-ensemble de
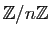 , noté
, noté 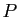 , constitué
des
, constitué
des
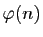 entiers premiers avec
entiers premiers avec  compris
entre
compris
entre 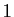 et
et  . Montrez ensuite
que l'application qui à
. Montrez ensuite
que l'application qui à 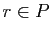 associe
associe 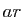 modulo
modulo  est une bijection de
est une bijection de 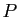 sur lui-même (raisonnez par l'absurde
et utilisez le lemme de Gauss).
Cela signifie que
sur lui-même (raisonnez par l'absurde
et utilisez le lemme de Gauss).
Cela signifie que
![$ \{ar [n] ,\;r\in P\}$](img912.gif) est égal à
est égal à 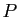 .
Maintenant faites le produit modulo
.
Maintenant faites le produit modulo  de tous les éléments de chacun des deux ensembles :
de tous les éléments de chacun des deux ensembles :
Allez, vous y êtes presque : un dernier coup de lemme de Gauss peut-être ?
Après un tel effort, vérifier que le codage RSA fonctionne, c'est presque du repos :
Puisque
![$ ed\equiv 1\;[\varphi(n)]$](img914.gif) , il existe un entier
, il existe un entier 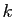 tel que
tel que
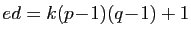 . Alors :
. Alors :
![$ (m^e)^d=m^{ed}=m (m^k)^{\varphi(n)}\equiv m\;[n]$](img916.gif) .
.
Euh... à condition que 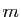 soit premier avec
soit premier avec  , pour pouvoir
appliquer le théorème ci-dessus à
, pour pouvoir
appliquer le théorème ci-dessus à 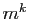 . Si
. Si 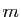 n'est pas premier avec
n'est pas premier avec  , il est divisible par
, il est divisible par 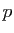 ou par
ou par 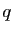 , mais pas les deux
(car il est inférieur à
, mais pas les deux
(car il est inférieur à 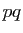 ). Supposons
qu'il soit divisible par
). Supposons
qu'il soit divisible par 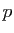 et écrivons :
et écrivons :
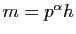 , où
, où 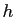 est premier avec
est premier avec 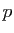 et avec
et avec 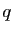 .
Allez, vous allez encore devoir travailler : montrez d'abord que
.
Allez, vous allez encore devoir travailler : montrez d'abord que
![$ p^{\alpha ed}\equiv p^\alpha \;[p]$](img920.gif) , puis que
, puis que
![$ p^{\alpha ed}\equiv p^\alpha \;[q]$](img921.gif) . Maintenant, vous pouvez en déduire que
. Maintenant, vous pouvez en déduire que
![$ p^{\alpha ed}\equiv p^\alpha \;[n]$](img922.gif) .
Recollez les morceaux :
.
Recollez les morceaux :
![$ m^{ed}=p^{\alpha ed} h^{ed}\equiv p^{\alpha} h \;[n]$](img923.gif) . Vous y êtes, le message est bien décodé !
Par pure bonté d'âme, nous vous dispensons de recommencer ce qui précède si
. Vous y êtes, le message est bien décodé !
Par pure bonté d'âme, nous vous dispensons de recommencer ce qui précède si 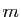 est multiple de
est multiple de 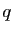 : merci qui ?
: merci qui ?
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() cet entier qui est censé être inférieur à
cet entier qui est censé être inférieur à ![]() .
Le codage le transforme en
.
Le codage le transforme en ![]() modulo
modulo ![]() . Pour décoder, il faut connaître
. Pour décoder, il faut connaître
![]() et calculer
et calculer ![]() modulo
modulo ![]() . Miracle, on retrouve
. Miracle, on retrouve ![]() .
Vous pouvez nous croire sur parole, mais ce serait dommage, car la démonstration
est parfaitement à votre portée.
.
Vous pouvez nous croire sur parole, mais ce serait dommage, car la démonstration
est parfaitement à votre portée.
![$\displaystyle \prod_{r\in P} ar =a^{\varphi(n)}\prod_{r\in P} r\equiv \prod_{r\in P} r\;[n]\;.
$](img913.gif)
![]() soit premier avec
soit premier avec ![]() , pour pouvoir
appliquer le théorème ci-dessus à
, pour pouvoir
appliquer le théorème ci-dessus à ![]() . Si
. Si ![]() n'est pas premier avec
n'est pas premier avec ![]() , il est divisible par
, il est divisible par ![]() ou par
ou par ![]() , mais pas les deux
(car il est inférieur à
, mais pas les deux
(car il est inférieur à ![]() ). Supposons
qu'il soit divisible par
). Supposons
qu'il soit divisible par ![]() et écrivons :
et écrivons :
![]() , où
, où ![]() est premier avec
est premier avec ![]() et avec
et avec ![]() .
Allez, vous allez encore devoir travailler : montrez d'abord que
.
Allez, vous allez encore devoir travailler : montrez d'abord que
![]() , puis que
, puis que
![]() . Maintenant, vous pouvez en déduire que
. Maintenant, vous pouvez en déduire que
![]() .
Recollez les morceaux :
.
Recollez les morceaux :
![]() . Vous y êtes, le message est bien décodé !
Par pure bonté d'âme, nous vous dispensons de recommencer ce qui précède si
. Vous y êtes, le message est bien décodé !
Par pure bonté d'âme, nous vous dispensons de recommencer ce qui précède si ![]() est multiple de
est multiple de ![]() : merci qui ?
: merci qui ?
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales