J'ai déjà démontré que ce qu'avance Abu Mohammed al-Khujandi - que Dieu soit miséricordieux avec lui - dans sa démonstration que la somme de deux nombres cubiques n'est pas un cube, est défectueux et incorrect.Pourquoi al-Khazin donne-t-il lui aussi une démonstration incomplète ? Cela reste un mystère. Un peu plus tard ibn Sina (plus connu comme médecin que comme mathématicien, sous le nom d'Avicenne) affirme lui aussi le résultat et précise qu'il n'a pas été démontré, puis ibn al-Khawam au XIe siècle affirme sans non plus la démontrer l'impossibilité du cas
Je suis quasi-persuadé queIl l'avait sans doute vérifié jusqu'àest premier quel que soit
. Je n'en ai pas la démonstration exacte, mais j'ai exclu si grande quantité de diviseurs par démonstrations infaillibles, et j'ai de si grandes lumières qui éclairent ma pensée, que j'aurais peine à me dédire.
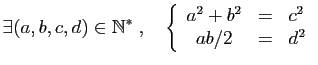 |
(P1) |
| (P2) |
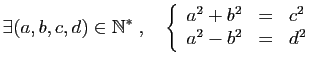 |
(P3) |
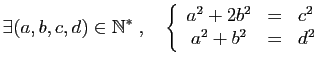 |
(P4) |
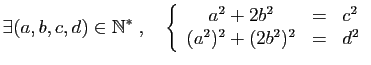 |
(P5) |
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales